Question

19．若定义在R上的偶函数f（x）满足f（x+2）=f（x），且当x∈[0，1]时，f（x）=x，则函数y=f（x）-log₃|x|的零点个数是（　　）

• A． 2
• B． 3
• C． 4
• D． 6

Answer 1

分析 在同一个坐标系中画出函数y=f（x）的图象与函数y=log₃|x|的图象，这两个函数图象的交点个数即为所求．

解答 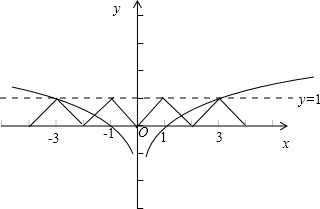解：∵偶函数f（x）满足f（x+2）=f（x），故函数的周期为2．
当x∈[0，1]时，f（x）=x，故当x∈[-1，0]时，f（x）=-x．
函数y=f（x）-log₃|x|的零点的个数等于函数y=f（x）的图象与函数y=log₃|x|的图象的交点个数．
在同一个坐标系中画出函数y=f（x）的图象与函数y=log₃|x|的图象，如图所示：
显然函数y=f（x）的图象与函数y=log₃|x|的图象有4个交点，
故选：C

点评 本题考查了根的存在性及根的个数判断，以及函数与方程的思想，根据函数零点和方程的关系进行转化是解决本题的关键．