练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知数列{an}，a1=20，an=an+1+2，求：
    （1）a5的值；
    （2）数列{an}的前n项和Sn．

    分析 （1）易得数列为等差数列，由首项和公差可得通项公式，当n=5时，求得a5=12；
    （2）根据等差数列的首项和公差即可写出数列的前n项和．

    解答 解：（1）数列{an}，a1=20，an=an+1+2，an+1-an=-2，
    数列{an}是以20为首项，以-2为公差的等差数列，
    an=20-2（n-1）=-2n+22，
    ∴an=-2n+22，
    当n=5时，a5=12；
    （2）数列{an}的前n项和Sn，Sn=$\frac{n（20-2n+22）}{2}$=（21-n）n，
    ∴Sn=（21-n）n．

    点评 本题考查等差数列的通项公式和前n项和公式，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．已知为虚数单位，复数z满足z=$\frac{1+i}{1-i}$，则z2=（　　）
    A．1B．-1C．2iD．-2i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．（B）已知等比数列{an}，首项为3，公比为$\frac{2}{5}$，前n项之积最大，则n=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设等比数列{an}的通项为an=$\frac{1}{n（n+1）}$，则其前10项的和S10等于（　　）
    A．$\frac{9}{10}$B．$\frac{11}{10}$C．$\frac{10}{9}$D．$\frac{10}{11}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．f（x+1）=$\sqrt{f（x）-{f}^{2}（x）}+\frac{1}{2}$，且f（1）=$\frac{1}{4}$，数列{an}满足an=f2（n）-f（n），n∈N*，若其前n项和为：-$\frac{35}{16}$，则n的值为（　　）
    A．16B．17C．18D．19

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．甲、乙二人进行乒乓球比赛，先胜4局者为胜，甲每局中获胜的概率为$\frac{3}{5}$．
    （1）求甲以4：1获胜的概率；
    （2）求比赛局数不多于5局的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知a＞0，且不等式（x+t+$\frac{1}{t}$+a）2+（x-$\frac{1}{t}$-2）2≥50对于任意实数x∈R，t＞0恒成立，则a的取值范围是（0，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

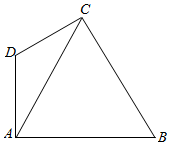    5．滨湖区拟建一主题游戏园，该游戏园为四边形区域ABCD，其中三角形区城ABC为主题活动区，其中∠ACB=60°，∠ABC=45°，AB=12$\sqrt{6}$m；AD、CD为游客通道（不考虑宽度），且∠ADC=120°，通道AD、CD围成三角形区域ADC为游客休闲中心，供游客休憩．
    （1）求AC的长度；
    （2）记游客通道AD与CD的长度和为L，求L的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设$\overrightarrow{a}$、$\overrightarrow{b}$是两个不平行的非零向量，且x（2$\overrightarrow{a}$+$\overrightarrow{b}$）+y（3$\overrightarrow{a}$-2$\overrightarrow{b}$）=7$\overrightarrow{a}$，x、y∈R，求实数x、y的值．

    查看答案和解析>>

    同步练习册答案