
分析 (Ⅰ)设椭圆C的焦距为2c,则F2(c,0),由点P,且F2在线段PF1的中垂线上,$e=\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,求出a,b,由此能求出椭圆C的方程.
(Ⅱ)由(Ⅰ)知F2(1,0),设直线l:y=k(x-2),与椭圆联立,得(1+2k2)x2-8k2x+8k2-2=0,由此利用根的判别式、韦达定理,结合已知条件能证明直线DF2与直线EF2的斜率之和为定值0.
解答 (本小题满分12分)
解:(Ⅰ)设椭圆C的焦距为2c,则F2(c,0)且a2=b2+c2,
由点P,且F2在线段PF1的中垂线上,得|PF2|=|F1F2|,
则$\sqrt{{{({2-c})}^2}+{{({\sqrt{3}})}^2}}=2c$,解得c=1,…(2分)
又∵$e=\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,∴$a=\sqrt{2}$,所以b=1,
∴所求椭圆C的方程为$\frac{x^2}{2}+{y^2}=1$.…(4分)
证明:(Ⅱ)由(Ⅰ)可知F2(1,0),
由题意可设直线l:y=k(x-2)与椭圆的交点D(x1,y1)、E(x2,y2)…(5分)
由$\left\{{\begin{array}{l}{\frac{x^2}{2}+{y^2}=1}\\{y=k({x-2})}\end{array}}\right.$,得$\frac{x^2}{2}+{k^2}{({x-2})^2}=1$,
整理得(1+2k2)x2-8k2x+8k2-2=0,
则$△=8-16{k^2}>0⇒{k^2}<\frac{1}{2}$,且$\left\{{\begin{array}{l}{{x_1}+{x_2}=\frac{{8{k^2}}}{{1+2{k^2}}}}\\{{x_1}{x_2}=\frac{{8{k^2}-2}}{{1+2{k^2}}}}\end{array}}\right.$,…(8分)
${k_{D{F_2}}}+{k_{E{F_2}}}=\frac{y_1}{{{x_1}-1}}+\frac{y_2}{{{x_2}-1}}=\frac{{k({{x_1}-2})}}{{{x_1}-1}}+\frac{{k({{x_2}-2})}}{{{x_2}-1}}$
=$\frac{{k[{({{x_1}-2})({{x_2}-1})+({{x_2}-2})({{x_1}-1})}]}}{{({{x_1}-1})({{x_2}-1})}}$=$\frac{{k[{2{x_1}{x_2}-3({{x_1}+{x_2}})+4}]}}{{({{x_1}-1})({{x_2}-1})}}$…(9分)
∵2x1x2-3(x1+x2)+4=$2×\frac{{8{k^2}-2}}{{1+2{k^2}}}-3×\frac{{8{k^2}}}{{1+2{k^2}}}+4$
=$\frac{{({16{k^2}-4})-24{k^2}+4+8{k^2}}}{{1+2{k^2}}}=0$…(11分)
∴${k_{D{F_2}}}+{k_{E{F_2}}}=0$,
即直线DF2与直线EF2的斜率之和为定值0.…(12分)
点评 本题考查椭圆方程的求法,考查直线的斜率之和为定值的证明,是中档题,解题时要认真审题,注意根的判别式、韦达定理、椭圆性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 311 | B. | 272 | C. | 144 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | 6 | C. | -$\frac{1}{6}$ | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
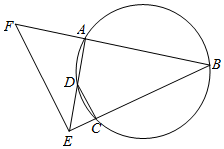 如图,A,B,C,D四点共圆,BC,AD的延长线交于点E,点F在BA的延长线上,
如图,A,B,C,D四点共圆,BC,AD的延长线交于点E,点F在BA的延长线上,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab-3a-b=0 | B. | ab-a-3b=0 | C. | ab-a-b=0 | D. | ab+a-b=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com