
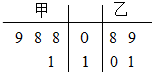
 甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.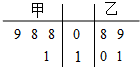 (Ⅰ)∵
(Ⅰ)∵. |
| x甲 |
| 1 |
| 4 |
| s | 2 甲 |
| 1 |
| 4 |
| 3 |
| 2 |
. |
| x乙 |
| 1 |
| 4 |
| 19 |
| 2 |
| s | 2 乙 |
| 1 |
| 4 |
| 19 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
| 5 |
| 4 |
. |
| x甲 |
. |
| x乙 |
| s | 2 甲 |
| s | 2 乙 |
| ||||
|
| 1 |
| 16 |
| ||||
|
| 1 |
| 8 |


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
| C、3 | ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 13 |
| 7 |
| 11 |
| 13 |
| 11 |
| 7 |
| 5 |
| 1 | ||||
|
| 1 | ||||
|
| ||||
| 2 |
| ||||
| 2 |
| 5 |
| 13 |
| 7 |
| 11 |
| A、综合法 | B、比较法 |
| C、反证法 | D、分析法 |
查看答案和解析>>
科目:高中数学 来源: 题型:
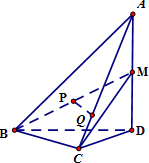 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.查看答案和解析>>
科目:高中数学 来源: 题型:
| 工种 健康状况 |
非油漆工 | 油漆工 | 合计 |
| 健康人数 | 28 | ||
| 患病人数 | 2 | 8 | |
| 合计 | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 长方体ABCD-A1B1C1D1的侧棱AA1=a,AB=2a,AA1=BC=a的矩形,E为C1D1的中点.
长方体ABCD-A1B1C1D1的侧棱AA1=a,AB=2a,AA1=BC=a的矩形,E为C1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
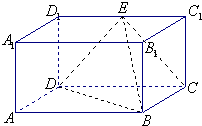
 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com