
分析 (1)化简可得a2n+1=2a2n+1,a2n=2a2n-1-1,从而可得(a2n+1-$\frac{1}{3}$)=4(a2n-1-$\frac{1}{3}$),从而判断;
(2)由(1)知a2n-1-$\frac{1}{3}$=$\frac{2}{3}$•4n-1,从而可得a2n-1+a2n=2•4n-1,从而分类讨论即可.
解答 解:(1)∵an+1=2an+(-1)n,
∴a2n+1=2a2n+(-1)2n,a2n=2a2n-1+(-1)2n-1,
即a2n+1=2a2n+1,a2n=2a2n-1-1,
a2n+1=2(2a2n-1-1)+1=4a2n-1-1,
即(a2n+1-$\frac{1}{3}$)=4(a2n-1-$\frac{1}{3}$),
∵a1-$\frac{1}{3}$=$\frac{2}{3}$≠0,
∴当λ=-$\frac{1}{3}$时,数列{a2n-1-$\frac{1}{3}$}是以$\frac{2}{3}$为首项,4为公比的等比数列,
(2)由题意知,a2n-1-$\frac{1}{3}$=$\frac{2}{3}$•4n-1,
故a2n-1=$\frac{2}{3}$•4n-1+$\frac{1}{3}$,故a2n=2($\frac{2}{3}$•4n-1+$\frac{1}{3}$)-1=$\frac{{4}^{n}}{3}$-$\frac{1}{3}$,
故a2n-1+a2n=2•4n-1,
①当n为奇数时,
Sn=1+3+5+11+…+$\frac{{4}^{\frac{n-1}{2}}}{3}$-$\frac{1}{3}$+$\frac{2}{3}$•${4}^{\frac{n-1}{2}}$+$\frac{1}{3}$
=2•${4}^{\frac{n-1}{2}}$+$\frac{2}{3}$•${4}^{\frac{n-1}{2}}$+$\frac{1}{3}$
=$\frac{8}{3}$•${4}^{\frac{n-1}{2}}$+$\frac{1}{3}$;
②当n为偶数时,
Sn=1+3+5+11+…+$\frac{{4}^{\frac{n}{2}}}{3}$-$\frac{1}{3}$=2•${4}^{\frac{n}{2}-1}$.
点评 本题考查了分类讨论的思想应用及构造法的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 2π???? | D. | 4$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
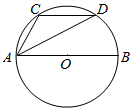 如图,AB是⊙O的直径,点C,D是半圆弧AB的三等分点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.(用a,b表示)
如图,AB是⊙O的直径,点C,D是半圆弧AB的三等分点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.(用a,b表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (1,2) | ||
| C. | ($\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$)或(-$\frac{\sqrt{5}}{5}$,-$\frac{2\sqrt{5}}{5}$) | D. | ($\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$)或(-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com