
分析 根据条件可以得出m,n满足的条件为$\left\{\begin{array}{l}{2m-3n≥-3}\\{3m-2n≤3}\\{m≥0}\\{n≥0}\end{array}\right.$,可以作出该不等式组所表示的平面区域,根据图形即可求出圆m2+n2=r2的半径的最大值,即得出$|\overrightarrow{a}|$的最大值.
解答 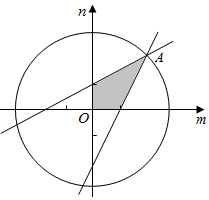 解:由$\overrightarrow{a}•\overrightarrow{b}≥-3$且$\overrightarrow{a}•\overrightarrow{c}≤3$得:$\left\{\begin{array}{l}{2m-3n≥-3}\\{3m-2n≤3}\\{m≥0}\\{n≥0}\end{array}\right.$;
解:由$\overrightarrow{a}•\overrightarrow{b}≥-3$且$\overrightarrow{a}•\overrightarrow{c}≤3$得:$\left\{\begin{array}{l}{2m-3n≥-3}\\{3m-2n≤3}\\{m≥0}\\{n≥0}\end{array}\right.$;
该不等式表示的平面区域如图阴影部分所示:
解$\left\{\begin{array}{l}{2m-3n=-3}\\{3m-2n=3}\end{array}\right.$得,$\left\{\begin{array}{l}{m=3}\\{n=3}\end{array}\right.$;
∴圆m2+n2=r2过A(3,3)时半径最大;
∴9+9=r2;
∴$r=3\sqrt{2}$,$|\overrightarrow{a}|=\sqrt{{m}^{2}+{n}^{2}}$;
∴$|\overrightarrow{a}|$的最大值为$3\sqrt{2}$.
故答案为:$3\sqrt{2}$.
点评 考查向量数量积的坐标运算,根据向量的坐标求向量的长度,以及能作出不等式组所表示的平面区域,线性规划的方法求最值.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6+2$\sqrt{3}$ | B. | 4$+3\sqrt{5}$ | C. | 9$+4\sqrt{5}$ | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |z1|<|z2| | B. | |z1|=|z2| | C. | |z1|>|z2| | D. | 无法比较 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
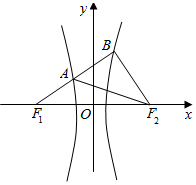 已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1,则双曲线C的离心率e的取值范围是( )
已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1,则双曲线C的离心率e的取值范围是( )| A. | (3,+∞) | B. | (1,2+$\sqrt{5}$) | C. | (3,2+$\sqrt{5}$) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p是真命题 | B. | 命题p的逆命题是真命题 | ||
| C. | 命题p的否命题是:若a<1,则a2≥1 | D. | 命题p的逆否命题是:若a2≥1,则a<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com