
如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.
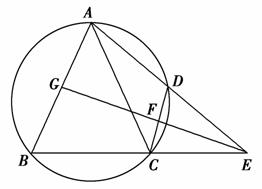
(1)证明:AB2=AD·AE;
(2)若EG平分∠AEB,且与AB、CD分别相交于点G、F,证明:∠CFG=∠BGF.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
已知函数f(x)=sinx+ex+x2010,令f1(x)=f ′(x),f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),则f2014(x)=( )
A.sinx+ex B.cosx+ex
C.-sinx+ex D.-cosx+ex
查看答案和解析>>
科目:高中数学 来源: 题型:
在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是1颗珠宝,第二件首饰由6颗珠宝(图中圆圈表示珠宝)构成如图1所示的正六边形,第三件首饰由15颗珠宝构成如图2所示的正六边形,第四件首饰是由28颗珠宝构成如图3所示的正六边形,第五件首饰是由45颗珠宝构成如图4所示的正六边形,以后每件首饰都在前一件上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断前10件首饰所用珠宝总颗数为( )
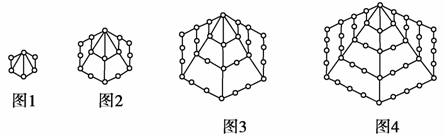
A.190 B.715
C.725 D.385
查看答案和解析>>
科目:高中数学 来源: 题型:
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.曲线C1的参数方程为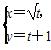 (t为参数),曲线C2的极坐标方程为ρsinθ-ρcosθ=3,则C1与C2的交点在直角坐标系中的坐标为________.
(t为参数),曲线C2的极坐标方程为ρsinθ-ρcosθ=3,则C1与C2的交点在直角坐标系中的坐标为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证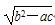 <
<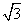 a”“索”的“因”应是( )
a”“索”的“因”应是( )
A.a-b>0 B.a-c>0
C.(a-b)(a-c)>0 D.(a-b)(a-c)<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com