
分析 令${y}_{1}=\sqrt{{r}^{2}-{x}^{2}},{y}_{2}=px+q$,y1表示半圆,y2表示直线,对?x∈[0,r],存在唯一的实数对(p,q),使不等式|y1-y2|≤t,几何意义为只有唯一的一条直线,
使得它在[0,r]上的每一个点,与圆在y轴方向上的距离始终不大于t,求得$({y}_{1}-{y}_{2})′=\frac{-x}{\sqrt{{r}^{2}-{x}^{2}}}-p$,分p≥0和p<0求出|y1-y2|得最大值点,联立$\left\{\begin{array}{l}{|p-q|=t}\\{|pr+q|=t}\end{array}\right.$,解得四个交点为(-1,r+t),(-1,r-t),($\frac{2t}{r}-1,r-t$),($-\frac{2t}{r}-1,r+t$),然后把四个点的坐标分别代入使$x=\sqrt{\frac{{p}^{2}{r}^{2}}{1+{p}^{2}}}$成立的不等式求得$\frac{t}{r}$.
解答 解:令${y}_{1}=\sqrt{{r}^{2}-{x}^{2}},{y}_{2}=px+q$,y1表示半圆,y2表示直线,
对?x∈[0,r],存在唯一的实数对(p,q),使不等式|y1-y2|≤t,
即存在唯一的实数对(p,q),使在[0,r]上,|y1-y2|max≤t,其几何意义为,只有唯一的一条直线,
使得它在[0,r]上的每一个点,与圆在y轴方向上的距离始终不大于t,
如图所示,阴影部分表示直线在区间[0,r]上的每一个点,与圆在y轴方向上的距离,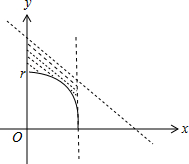
$({y}_{1}-{y}_{2})′=\frac{-x}{\sqrt{{r}^{2}-{x}^{2}}}-p$,如果p≥0,则(y1-y2)′≤0,在x=0或x=r时,|y1-y2|有最大值,
如果p<0,那么y1-y2在[0,r]上先单调递增后单调递减,令(y1-y2)′=0,得$x=\sqrt{\frac{{p}^{2}{r}^{2}}{1+{p}^{2}}}$,
在x=0或x=r或$x=\sqrt{\frac{{p}^{2}{r}^{2}}{1+{p}^{2}}}$时,|y1-y2|有最大值,
∴|y1-y2|max≤t恒成立,必须有x=0或x=r或$x=\sqrt{\frac{{p}^{2}{r}^{2}}{1+{p}^{2}}}$时都有|y1-y2|≤t,
∴$\left\{\begin{array}{l}{|q-r|≤t}\\{|pr+q|≤t}\\{|(p|p|-1)\sqrt{\frac{{r}^{2}}{1+{p}^{2}}}+q|≤t}\end{array}\right.$,
∵(p,q)的唯一性,∴上述不等式组有唯一解,
将p,q看作自变量和因变量,上述线性规划问题的可行域只有一个点,前两个约束条件对应的是两个带状图形,
它们的交集是一个平行四边形,联立$\left\{\begin{array}{l}{|p-q|=t}\\{|pr+q|=t}\end{array}\right.$,解得四个交点为(-1,r+t),(-1,r-t),($\frac{2t}{r}-1,r-t$),($-\frac{2t}{r}-1,r+t$),
∵可行域只有一个点,∴这个点一定使第三个不等式等号成立,
将(-1,r+t)代入得,$|-\sqrt{2}r+r+t|=t$,∵r≠0,∴($\sqrt{2}-1$)r=2t,得$\frac{t}{r}=\frac{\sqrt{2}-1}{2}$;
将(-1,r-t)代入得,$|-\sqrt{2}r+r-t|=t$,∵r>0,t>0,∴不合题意;
将($\frac{2t}{r}-1,r-t$)代入得,$|r+t-r\sqrt{1+(\frac{2t}{r}+1)^{2}}|=t$,无解;
将($-\frac{2t}{r}-1,r+t$)代入得,$|r-t-r\sqrt{1+(\frac{2t}{r}-1)^{2}}|=t$,无解.
p>0时,t>2r,如果取等,在图形中,相当于直线在区间[0,r]上的某点与圆在y轴方向上的距离大于2r,不合题意.
综上,$\frac{t}{r}$=$\frac{\sqrt{2}-1}{2}$.
故答案为:$\frac{\sqrt{2}-1}{2}$.
点评 本题考查恒成立问题,考查了数学转化思想方法,考查数形结合的解题思想方法,题目设置难度较大.


科目:高中数学 来源: 题型:选择题
| A. | a<-1或a>0 | B. | -1<a<0 | C. | a<0或a>1 | D. | a<-1或a>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com