
分析 (Ⅰ)由an+1=3an+2,变形为an+1+1=3(an+1),利用等比数列的定义及其通项公式即可得出.
(Ⅱ)利用“裂项求和”方法即可得出.
解答 (Ⅰ)证明:由an+1=3an+2⇒an+1+1=3(an+1).…(1分)
∵a1=2,∴a1+1=3≠0且an+1≠0.…(2分)
∴$\frac{{{a_{n+1}}+1}}{{{a_n}+1}}=3$.…(3分)
所以{an+1}是首项为3公比为3的等比数列.…(4分)${a_n}+1=3•{3^{n-1}}={3^n}$,得${a_n}={3^n}-1$.
即{an}的通项公式是${a_n}={3^n}-1$.…(6分)
(Ⅱ)解:$\frac{3}{{{a_1}{a_2}}}+\frac{3^2}{{{a_2}{a_3}}}+…+\frac{3^n}{{{a_n}{a_{n+1}}}}=\frac{3}{{(3-1)({3^2}-1)}}+\frac{3^2}{{({3^2}-1)({3^3}-1)}}+…+\frac{3^n}{{({3^n}-1)({3^{n+1}}-1)}}$
=$\frac{1}{2}[(\frac{1}{3-1}-\frac{1}{{{3^2}-1}})+(\frac{1}{{{3^2}-1}}-\frac{1}{{{3^3}-1}})+…+(\frac{1}{{{3^n}-1}}-\frac{1}{{{3^{n+1}}-1}})]$…(9分)
=$\frac{1}{2}(\frac{1}{2}-\frac{1}{{{3^{n+1}}-1}})=\frac{1}{4}-\frac{1}{{2({3^{n+1}}-1)}}$.…(11分)
∴${S_n}=\frac{1}{4}-\frac{1}{{2({3^{n+1}}-1)}}$.…(12分)
点评 本题考查了“裂项求和方法”、等比数列的通项公式的定义及其通项公式,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
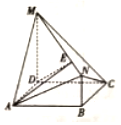 如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.
如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6米/秒 | B. | 7米/秒 | C. | 8米/秒 | D. | 9米/秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
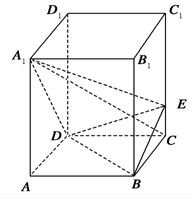 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com