
分析 函数f(x)=|xex|-m(m∈R)有三个零点,转化为方程|xex|=m有三个不相等的实数解,即y=m与函数y=|xex|的图象有三个交点,利用导数法分析f(x)=xex的单调性和极值,进而结合函数图象的对折变换画出函数y=|xex|的图象,数形结合可得答案.
解答 解:函数f(x)=|xex|-m(m∈R)有三个零点,令g(x)=xex,则g′(x)=(1+x)ex,
当x<-1时,g′(x)<0,当x>-1时,g′(x)>0,
故g(x)=xex在(-∞,-1)上为减函数,在(-1,+∞)上是减函数,
g(-1)=-$\frac{1}{e}$,
又由x<0时,g(x)<0,当x>0时,g(x)>0,
故函数y=|xex|的图象如下图所示:
故当m∈(0,$\frac{1}{e}$)时,y=m与函数y=|xex|的图象有三个交点,
即方程|xex|=m有三个不相等的实数解,
故m的取值范围是(0,$\frac{1}{e}$),
故答案为:(0,$\frac{1}{e}$).
点评 本题考查的知识点是根的存在性及根的个数,函数的极值的求法,其中结合函数图象的对折变换画出函数y=|xex|的图象,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{{\sqrt{3}}}{3},1})$ | B. | $[{\frac{1}{3},\frac{1}{2}}]$ | C. | $[{\frac{{\sqrt{3}}}{3},\frac{{\sqrt{2}}}{2}})$ | D. | $({0,\frac{{\sqrt{2}}}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | l | C. | -l | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )
如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )| A. | i≤1009 | B. | i>1009 | C. | i≤1010 | D. | i>1010 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:填空题
若数列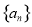 满足
满足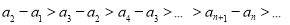 ,则称数列
,则称数列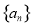 为“差递减”数列.若数列
为“差递减”数列.若数列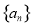 是“差递减”数列,且其通项
是“差递减”数列,且其通项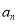 与其前
与其前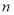 项和
项和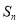 (
( )满足
)满足 (
( ),则实数
),则实数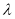 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com