
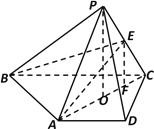
【题目】在四棱锥PABCD中,AD∥BC,平面PAC⊥平面ABCD,AB=AD=DC=1,
∠ABC=∠DCB=60,E是PC上一点.
(Ⅰ)证明:平面EAB⊥平面PAC;
(Ⅱ)若△PAC是正三角形,且E是PC中点,求三棱锥AEBC的体积.

【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)在等腰梯形ABCD中,由条件得AB⊥AC,又平面PAC⊥平面ABCD,故得AB⊥平面PAC,从而可得平面EAB⊥平面PAC.(Ⅱ)根据![]() 求解,由(Ⅰ)得AB⊥平面PAC,故AB为三棱锥BEAC的高,在正△PAC中可得S△EAC=
求解,由(Ⅰ)得AB⊥平面PAC,故AB为三棱锥BEAC的高,在正△PAC中可得S△EAC=![]() S△PAC,根据体积公式可求得三棱锥的体积.
S△PAC,根据体积公式可求得三棱锥的体积.
试题解析:
(Ⅰ)证明:依题意得四边形ABCD是底角为60的等腰梯形,
∴∠BAD=∠ADC=120.
∵ AD=DC,
∴∠DAC=∠DCA=30,
∴∠BAC=∠BAD∠DAC=12030=90,
∴AB⊥AC.
∵平面PAC⊥平面ABCD, 平面PAC∩平面ABCD=AC,
∴AB⊥平面PAC.
又AB平面EAB,
∴平面EAB⊥平面PAC.
(Ⅱ)由(Ⅰ)及已知得,在Rt△ABC中,∠ABC=60,AB=1,
∴AC= ABtan60=![]() ,且BC=2AB=2.
,且BC=2AB=2.
又AB⊥平面PAC,
∴AB是三棱锥BEAC的高.
∵E是PC的中点,
∴S△EAC=![]() S△PAC=
S△PAC=![]() .
.
∴三棱锥AEBC的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】定义在(0,+∞)上的单调函数f(x),x∈(0,+∞),f[f(x)﹣lnx]=1,则方程f(x)﹣f′(x)=1的解所在区间是 ( )
A. (2,3) B. ![]() C.
C. ![]() D. (1,2)
D. (1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车因绿色、环保、健康的出行方式,在国内得到迅速推广.最近,某机构在某地区随机采访了10名男士和10名女士,结果男士、女士中分别有7人、6人表示“经常骑共享单车出行”,其他人表示“较少或不选择骑共享单车出行”.
(1)从这些男士和女士中各抽取一人,求至少有一人“经常骑共享单车出行”的概率;
(2)从这些男士中抽取一人,女士中抽取两人,记这三人中“经常骑共享单车出行”的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,其焦距为2,离心率为
,其焦距为2,离心率为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆的右焦点为![]() ,
, ![]() 为
为![]() 轴上一点,满足
轴上一点,满足![]() ,过点
,过点![]() 作斜率不为0的直线
作斜率不为0的直线![]() 交椭圆于
交椭圆于![]() 两点,求
两点,求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,
, ![]() (
(![]() 在
在![]() 轴上方),且
轴上方),且![]() .设点
.设点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,三角形
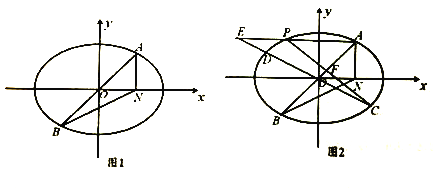
,三角形![]() 的面积为2(如图1).
的面积为2(如图1).
(1)求椭圆的方程;
(2)设平行于![]() 的直线与椭圆相交,其弦的中点为
的直线与椭圆相交,其弦的中点为![]() .
.
①求证:直线![]() 的斜率为定值;
的斜率为定值;
②设直线![]() 与椭圆相交于两点
与椭圆相交于两点![]() ,
, ![]() (
(![]() 在
在![]() 轴上方),点
轴上方),点![]() 为椭圆上异于
为椭圆上异于![]() ,
, ![]() ,
, ![]() ,
, ![]() 一点,直线
一点,直线![]() 交
交![]() 于点
于点![]() ,
, ![]() 交
交![]() 于点
于点![]() ,如图2,求证:
,如图2,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心为
是圆心为![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的点,
上的点, ![]() 为曲线
为曲线![]() 上的点,求
上的点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018贵州遵义市高三上学期第二次联考】设抛物线![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,抛物线的焦点为
,抛物线的焦点为![]() ,以
,以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆与抛物线的一个交点为
的椭圆与抛物线的一个交点为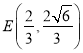 ;自
;自![]() 引直线交抛物线于
引直线交抛物线于![]() 两个不同的点,设
两个不同的点,设![]() .
.
(Ⅰ)求抛物线的方程和椭圆的方程;
(Ⅱ)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com