
(本题满分15分)如图,在四面体ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,
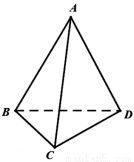
(1)求证:AC⊥BD;
(2)若平面ABD⊥平面CBD,且BD=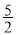 ,求二面角C-AD-B的余弦值。
,求二面角C-AD-B的余弦值。
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2016届安徽省等高三第三次联考文科数学卷(解析版) 题型:解答题
已知函数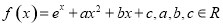 .
.
(1)若曲线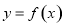 在点
在点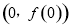 处的切线方程为
处的切线方程为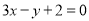 ,求
,求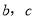 的值;
的值;
(2)若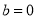 ,且
,且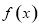 在
在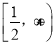 上单调递增,求实数
上单调递增,求实数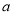 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年浙江慈溪中学高二2-10班上期中数学卷(解析版) 题型:选择题
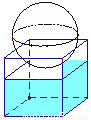
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )
A.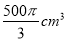 B.
B.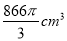 C.
C.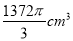 D.
D.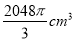
查看答案和解析>>
科目:高中数学 来源:2015-2016学年黑龙江齐齐哈尔实验中学高一上期中数学卷(解析版) 题型:解答题
已知函数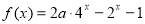 .
.
(1)当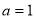 时,求函数
时,求函数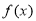 的零点;
的零点;
(2)若函数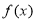 有零点,求实数
有零点,求实数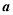 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁沈阳二中高二12月月考文科数学卷(解析版) 题型:解答题
已知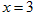 是函数
是函数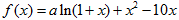 的一个极值点.
的一个极值点.
(Ⅰ)求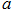 ;
;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若直线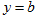 与函数
与函数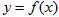 的图像有
的图像有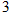 个交点,求
个交点,求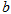 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年山西省高二11月月考理科数学卷(解析版) 题型:填空题
如图所示,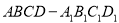 为正方体,给出以下五个结论:
为正方体,给出以下五个结论:

①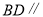 平面
平面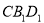 ;
;
②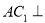 平面
平面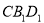 ;
;
③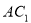 与底面
与底面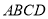 所成角的正切值是
所成角的正切值是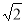 ;
;
④二面角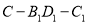 的正切值是
的正切值是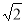 ;
;
⑤过点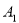 且与异面直线
且与异面直线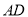 和
和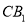 均成
均成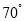 角的直线有2条.
角的直线有2条.
其中,所有正确结论的序号为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com