Question

20．已知函数$g（x）=2sin（2ωx+\frac{π}{6}）$（其中0＜ω＜1），若点$（-\frac{π}{6}，0）$是函数g（x）图象的一个对称中心，
（1）试求ω的值；
（2）若f（x）=g（x）+1，请先列表再作出函数f（x）在区间x∈[-π，π]上的图象．

Answer 1

分析 （1）根据三角函数的对称性即可求出ω的值．
（2）用五点法作出函数在区间[-π，π]上的图象．

解答 解：（1）∵点$（-\frac{π}{6}，0）$是函数g（x）图象的一个对称中心，
∴$-\frac{π}{6}$×2ω+$\frac{π}{6}$=kπ，
即ω=$\frac{1}{2}$-3k，
∵0＜ω＜1，∴当k=0时，ω=$\frac{1}{2}$．
（2）∵ω=$\frac{1}{2}$，则g（x）=2sin（x+$\frac{π}{6}$），
∴f（x）=g（x）+1=2sin（x+$\frac{π}{6}$）+1，
列表

x+$\frac{π}{6}$	-$\frac{5π}{6}$	-$\frac{π}{2}$	0	$\frac{π}{2}$	π	$\frac{7π}{6}$
x	-π	-$\frac{2π}{3}$	-$\frac{π}{6}$	$\frac{π}{3}$	$\frac{5π}{6}$	π
f（x）	0	-1	1	3	1	0

如图所示：

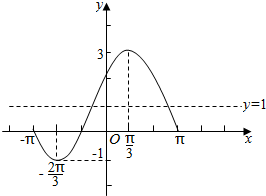
点评 本题主要考查三角函数对称性的应用，已经三角函数函数图象的作法，要求熟练掌握用五点法作出函数y=Asin（ωx+φ）在一个周期上的简图，属于中档题．