
分析 写出所给的三个复数的表示式,根据代数形式的表示式写出复数对应的点的坐标,即得到三角形的三个顶点的坐标,求出三角形的面积.
解答 解:设Z=x+yi(x,y∈R),由题意得Z2=(x-y)2=x2-y2+2xyi
∴$\left\{\begin{array}{l}{\sqrt{{x}^{2}+{y}^{2}}=\sqrt{2}}&{①}\\{2xy=1}&{②}\end{array}\right.$
故(x-y)2=0,∴x=y将其代入②得2x2=2,
∴x=±1
故 $\left\{\begin{array}{l}x=1\\ y=1\end{array}\right.$ 或 $\left\{\begin{array}{l}x=-1\\ y=-1\end{array}\right.$
故Z=1+i或Z=-1-i;
(2)当Z=1+i时,Z2=2i,Z-Z2=1-i
所以A(1,1),B(0,2),C(1,-1)
∴$|{AC}|=2,{S_{△ABC}}=\frac{1}{2}×1×2=1$
当Z=-1-i时,Z2=2i,Z-Z2=-1-3i,A(-1,-1),B(0,2),C(-1,3),
S△ABC=$\frac{1}{2}$×4×2=4,
即△ABC的面积为4或1,
故答案为:4或1,
点评 本题考查三角形面积的计算,根据条件先求出复数,结合复数的几何意义求出对应点的坐标是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\frac{3+\sqrt{5}}{2}$ | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\frac{3+\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,$\frac{3}{2}$] | B. | [-$\frac{3}{2}$,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,3] | D. | (-3,-$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 12 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (-∞,2] | C. | (2,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
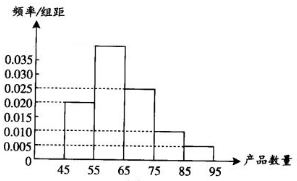 为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为0.4;这20名工人中一天生产该产品数量在[55,75)的人数是13.
为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为0.4;这20名工人中一天生产该产品数量在[55,75)的人数是13.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com