
 某物流公司运费计算框图如图所示,其中d为按运送里程给运费打的折扣,n为运送物品的件数.现有顾客办理A、B两件物品递送,其中A物品运送单价为p1=0.02元/千克•千米,重量为w1=5千克,运送里程为s1=250千米;B物品运送单价为p2=0.03元/千克•千米,重量为w2=6千克,运送里程为s2=500千米.则按运费计算框图算出该顾客应付运费sum=( )
某物流公司运费计算框图如图所示,其中d为按运送里程给运费打的折扣,n为运送物品的件数.现有顾客办理A、B两件物品递送,其中A物品运送单价为p1=0.02元/千克•千米,重量为w1=5千克,运送里程为s1=250千米;B物品运送单价为p2=0.03元/千克•千米,重量为w2=6千克,运送里程为s2=500千米.则按运费计算框图算出该顾客应付运费sum=( )| A、94.5元 | B、97元 |
| C、103.5元 | D、106元 |


科目:高中数学 来源: 题型:
 某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如图所示茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.
某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如图所示茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.查看答案和解析>>
科目:高中数学 来源: 题型:
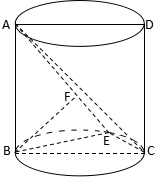 如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、-
| ||
C、
| ||
D、-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com