Question

【题目】如图，四棱锥中，⊥平面，底面为正方形，为的中点，.

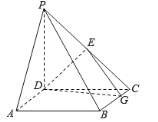
（1）求证：；

（2）边上是否存在一点，使得//平面？若存在，求的长，若不存在，请说明理由.

Answer 1

【答案】（1）见解析；（2）23.

【解析】分析：（1）要证明，需证面，需证：，用分析法书写即可。

（2）连结AC,取AC中点O,连结EO,GO,延长GO交AD于点M,则PA∥平面MEG，再求解

详解：(Ⅰ)证明：∵PD⊥平面ACD，∴PD⊥BC

又∵ABCD是正方形∴BC⊥CD

∵PD∩CD=D

∴BC⊥平面PCD

又∵PC面PBC

∴PC⊥BC

（2）连结AC,取AC中点O,连结EO,GO,延长GO交AD于点M,则PA∥平面MEG

下面证明之

∵E为PC的中点，O是AC的中点，

∴EO∥PA,

又∵EO平面MEG，PA平面MEG

∴PA∥平面MEG

在正方形ABCD中,∵O是AC的中点,∴△OCG≌△OAM，

∴AM=CG=23,∴所求AM的长为23.