
分析 (1)先求导,再分类讨论,利用导数和函数单调性关系即可求出,
(2)原不等式等价于(e-x-1)(αx+1)+x≥0,再构造函数,利用函数和最值得关系即可证明
解答 解:(l)y=f(x)+g(x)=ex+ax+b,x∈R,y'=ex+a,
若a≥0,则y'>0所以函数y=f(x)+g(x)的单调增区间为(-∞,+∞),
若a<0,令y'>0,得x>ln(-a),令y'<0,得x<ln(-a),
所以函数y=f(x)+g(x)的单调增区间为(ln(-a),+∞),单调减区间为(-∞,ln(-a))
(2)当$0≤a≤\frac{1}{2},b=1$,x≥0时,
要证$\frac{1}{f(x)}+\frac{x}{g(x)}≥1$,
即证${e^{-x}}+\frac{x}{ax+1}≥1$,
即证e-x(ax+1)+x≥ax+1,
即证(e-x-1)(αx+1)+x≥0,
设h(x)=(e-x-1)(ax+1)+x,则h(0)=0,h'(x)=e-x(a-1-ax)+1-a,
下证ex≥x+1,令ϕ(x)=ex-x-1,则ϕ'(x)=ex-1,
当x∈(-∞,0)时,ϕ'(x)<0;
当x∈(0,+∞)时,ϕ'(x)>0,
所以[ϕ(x)]min=ϕ(0)=0,
所以ex≥x+1,即-x≥1-ex,
所以h'(x)=e-x(a-1-ax)+1-a≥e-x[a-1+a(1-ex)]+1-a=e-x(2a-1)+1-2a=(e-x-1)(2a-1)≥0,
所以h(x)在[0+∞)上单调递增,所以h(x)≥h(0)=0,
所以当x≥0时,$\frac{1}{f(x)}+\frac{x}{g(x)}≥1$.
点评 本题是一道导数的综合题,考查了函数单调性和导数之间的关系以及,利用导数求函数的单调区间,等价转化思想,不等式的证明.综合性较强,难度较大.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,α⊥β,则l⊥β | B. | 若l∥α,α∥β,则l∥β | C. | 若l⊥α,α∥β,则l⊥β | D. | 若l⊥α,α⊥β,则l∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
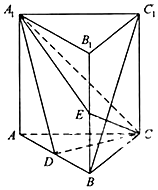 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com