
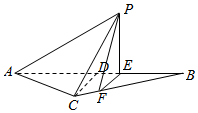
 等腰△ABC的底边$AB=6\sqrt{6}$,高CD=3,点E是线段BD上异于点B,D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
等腰△ABC的底边$AB=6\sqrt{6}$,高CD=3,点E是线段BD上异于点B,D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.分析 (Ⅰ)证明EF⊥PE,而AB∩PE=E,EF⊥AB,即可证明EF⊥平面PAE;
(Ⅱ)记BE=x,V(x)表示四棱锥P-ACFE的体积,求出底面面积,可得体积,即可求V(x)的最值.
解答 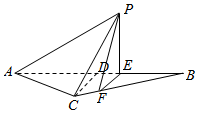 (Ⅰ)证明:∵EF⊥AB,∴∠BEF=∠PEF=90°,
(Ⅰ)证明:∵EF⊥AB,∴∠BEF=∠PEF=90°,
故EF⊥PE,而AB∩PE=E,
所以EF⊥平面PAE.
(Ⅱ)解:∵PE⊥AE,PE⊥EF,
∴PE⊥平面ABC,即PE为四棱锥P-ACFE的高.
由高线CD及EF⊥AB得EF∥CD,∴$\frac{BE}{BD}=\frac{EF}{CD}$,
由题意知$\frac{x}{{3\sqrt{6}}}=\frac{EF}{3}∴EF=\frac{{\sqrt{6}}}{6}x$
∴${S_{ACFE}}={S_{△ABC}}-{S_{△BEF}}=\frac{1}{2}×6\sqrt{6}×3-\frac{1}{2}×\frac{{\sqrt{6}}}{6}{x^2}$=$9\sqrt{6}-\frac{{\sqrt{6}}}{12}{x^2}$.
而PE=EB=x,∴$V(x)=\frac{1}{3}{S_{ACFE}}•PE=3\sqrt{6}x-\frac{{\sqrt{6}}}{36}{x^3}$,$(0<x<3\sqrt{6})$
∴当x=6时V(x)max=V(6)=$12\sqrt{6}$.
点评 本题考查三视图,考查线面垂直的证明,考查体积的计算,考查学生分析解决问题的能力,属于中档题.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | 丁酉年 | B. | 戊未年 | C. | 乙未年 | D. | 丁未年 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | (0,$\frac{5}{2}$] | C. | [$\frac{5}{2}$,4] | D. | [$\frac{5}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
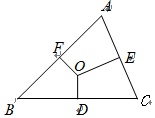 如图,在△ABC中,BC=a,AC=b,AB=c.O是△ABC的外心,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,则OD:OE:OF等于( )
如图,在△ABC中,BC=a,AC=b,AB=c.O是△ABC的外心,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,则OD:OE:OF等于( )| A. | a:b:c | B. | $\frac{1}{a}:\frac{1}{b}:\frac{1}{c}$ | C. | sinA:sinB:sinC | D. | cosA:cosB:cosC |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com