
(本小题满分12分)
设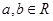 ,且
,且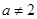 ,定义在区间
,定义在区间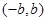 内的函数
内的函数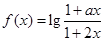 是奇函数.
是奇函数.
(1)求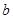 的取值范围;
的取值范围;
(2)讨论函数 的单调性并证明.
的单调性并证明.
(1)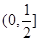 . (2)
. (2) 在(-b,b)内是减函数,具有单调性.
在(-b,b)内是减函数,具有单调性.
解析试题分析:(1)由函数f(x)在区间(-b,b)是奇函数,知f(-x)=-f(x),x∈(-b,b)上恒成立,用待定系数法求得a;同时函数要有意义,即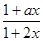 >0,x∈(-b,b)上恒成立,可解得结果.
>0,x∈(-b,b)上恒成立,可解得结果.
(2)选用定义法求解,先任意取两个变量且界定大小,再作差变形看符号.
解 (1)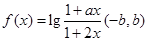 是奇函数等价于:
是奇函数等价于:
对任意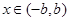 都有
都有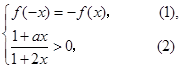 …………………2分
…………………2分
(1)式即为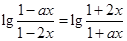 ,由此可得
,由此可得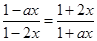 ,也即
,也即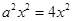 ,…………………4分
,…………………4分
此式对任意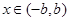 都成立相当于
都成立相当于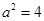 ,因为
,因为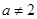 ,所以
,所以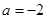 ,
,
代入②式,得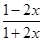 >0,即
>0,即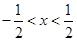 ,此式对任意
,此式对任意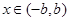 都成立相当于
都成立相当于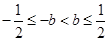 ,…………………6分
,…………………6分
所以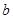 的取值范围是
的取值范围是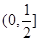 .…………………7分
.…………………7分
(2)设任意的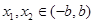 ,且
,且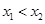 ,由
,由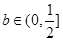 ,得
,得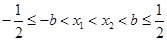 ,
,
所以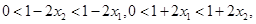 …………………9分
…………………9分
从而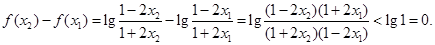

因此 在(-b,b)内是减函数,具有单调性. …………………12分
在(-b,b)内是减函数,具有单调性. …………………12分
考点:本试题主要考查了函数的奇偶性,还考查了用定义法证明函数的单调性的运用。
点评:解决该试题的关键是要注意定义域优先考虑原则,以及作差时的变形要到位,要用上两个变量的大小关系。


科目:高中数学 来源: 题型:解答题
海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里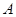 处,如图,现假设:①失事船的移动路径可视为抛物线
处,如图,现假设:①失事船的移动路径可视为抛物线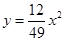 ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发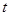 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为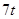

(1)当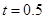 时,写出失事船所在位置
时,写出失事船所在位置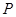 的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可)
的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可)
(2)问救援船的时速至少是多少海里才能追上失事船?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设f(x)=2x3+ax2+bx+1的导数为f′(x),若函数y=f′(x)的图象关于直线x=-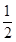 对称,且f′(1)=0.
对称,且f′(1)=0.
(1)求实数a,b的值;
(2)讨论函数f(x)的单调性,并求出单调区间 。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)已知函数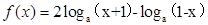 其中a>0,且a≠1,
其中a>0,且a≠1,
(1)求函数 的定义域;
的定义域;
(2)当0<a<1时,解关于x的不等式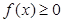 ;
;
(3)当a>1,且x∈[0,1)时,总有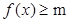 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数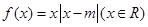 ,且
,且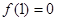 .
.
(Ⅰ)求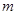 的值,并用分段函数的形式来表示
的值,并用分段函数的形式来表示 ;
;
(Ⅱ)在如图给定的直角坐标系内作出函数 的草图;
的草图;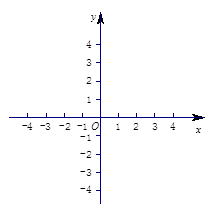
(III)由图象写出函数 的奇偶性及单调区间.
的奇偶性及单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
已知函数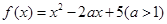 .
.
(1) 若函数 的定义域和值域均为
的定义域和值域均为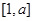 ,求实数
,求实数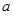 的值;
的值;
(2) 若 在区间
在区间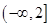 上是减函数,且对任意的
上是减函数,且对任意的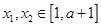 ,
,
总有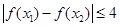 ,求实数
,求实数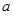 的取值范围;
的取值范围;
(3) 若 在
在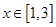 上有零点,求实数
上有零点,求实数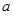 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com