
已知函数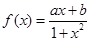 是定义域为
是定义域为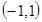 上的奇函数,且
上的奇函数,且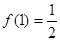
(1)求 的解析式,
的解析式,
(2)用定义证明: 在
在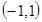 上是增函数,
上是增函数,
(3)若实数 满足
满足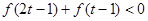 ,求实数
,求实数 的范围.
的范围.
(1)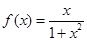 ;(2)见解析;(3) 0<
;(2)见解析;(3) 0<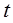 <
<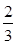
 。
。
解析试题分析:(1)先根据f(x)为奇函数,知f(0)=0,可得b=0,然后再根据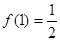 ,求出a值.从而确定f(x)的解析式.
,求出a值.从而确定f(x)的解析式.
(2)用单调性定义证明函数单调性的步骤有三:一是取值.二是作差变形,判断符号;三是得出结论.
(3)解此类抽象不等式关键是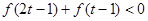 ∴
∴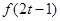 <-
<-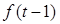 ,再根据奇函数转化为
,再根据奇函数转化为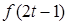 <
<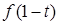 ,再利用单调性脱掉法则符号f,从而转化为自变量之间的大小关系即可解决.
,再利用单调性脱掉法则符号f,从而转化为自变量之间的大小关系即可解决.
(1) ∵函数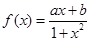 是定义域为
是定义域为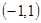 上的奇函数 ∴
上的奇函数 ∴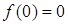
∴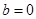 ——————————2
——————————2
又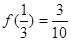 ∴
∴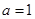
∴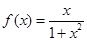 ——————————————4
——————————————4
(2)任取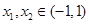 且
且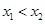
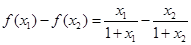
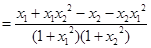
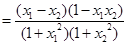 ————————6
————————6
∵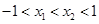 ∴
∴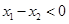
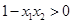
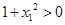
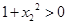
∴ 即
即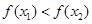
∴  在
在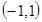 上是增函数————————————8
上是增函数————————————8
(3)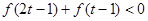 ∴
∴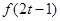 <-
<-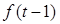
又由已知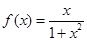 是
是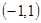 上的奇函数
上的奇函数
∴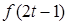 <
<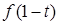 ----------------------10
----------------------10
∵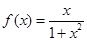 是
是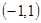 上的增函数
上的增函数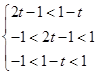 ————————————13
————————————13
∴0<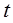 <
<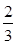
 --------------------------------14
--------------------------------14
考点:本小题考查函数的奇偶性和单调性以及解抽象不等式等知识.
点评: 当奇函数的定义域内有0时,要注意f(0)=0这个条件的使用.利用单调性定义进行证明时,关键是作差变形确定差值符号,一般要分解成若干个因式积的形式,通过判断每个因式的符号来判断差值符号.
在解抽象不等式时,要注意利用单调性把函数值的大小关系转化为自变量之间的大小关系从而转化为普通不等式来解.


科目:高中数学 来源: 题型:解答题
(附加题)本小题满分10分
已知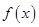 是定义在
是定义在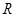 上单调函数,对任意实数
上单调函数,对任意实数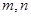 有:
有: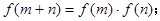 且
且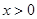 时,
时,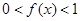 .
.
(1)证明: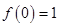 ;
;
(2)证明:当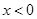 时,
时,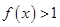 ;
;
(3)当 时,求使
时,求使 对任意实数
对任意实数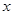 恒成立的参数
恒成立的参数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(16分)已知函数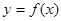 是定义在
是定义在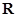 上的奇函数,且当
上的奇函数,且当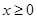 时,
时, .
.
(1)当 时,求函数
时,求函数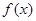 的解析式;
的解析式;
(2)若函数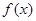 为单调递减函数;
为单调递减函数;
①直接写出 的范围(不必证明);
的范围(不必证明);
②若对任意实数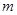 ,
,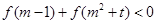 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1
(1)求f(1)的值
(2)若满足f(x) +f(x-8)≤2 求x的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com