
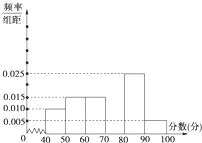
 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题: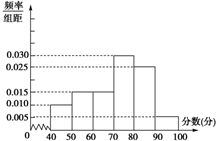 解:(1)∵频率分布直方图中各组的频率和等于1,
解:(1)∵频率分布直方图中各组的频率和等于1,

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
| 小米手机 | 红米手机 | 黑米手机 | |
| 经济型 | 240 | x | y |
| 豪华型 | 160 | 80 | z |
查看答案和解析>>
科目:高中数学 来源: 题型:
| QC |
| PC |
| PQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,AC=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,AC=1,BC=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
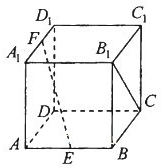 如图,在正方体ABCD-A1B1C1D1中,AB=2,点E、F分别是AB、A1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,AB=2,点E、F分别是AB、A1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 优秀 | 合格 | 总计 | |
| 男生 | 6 | ||
| 女生 | 18 | ||
| 总计 | 60 |
| 1 |
| 3 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com