
分析 (1)先确定函数f(x)的定义域,然后对函数f(x)求导,根据导函数大于0时原函数单调递增,导函数小于0时原函数单调递减求出单调区间.
(2)分别表示出函数h(x)=-f(x)、g(x)的值域,根据f(x)的值域应为g(x)的值域的子集可得答案.
解答 解:(1)f(x)=lnx-ax,
∴x>0,即函数f(x)的定义域为(0,+∞)
∴当a≤0时,f(x)在(0,+∞)上是增函数
当a>0时,∵f'(x)=$\frac{1}{x}$-a=$\frac{1-ax}{x}$,
∵f′(x)>0,则1-ax>0,ax<1,x<$\frac{1}{a}$,f′(x)<0,则1-ax<0,ax>1,
x>$\frac{1}{a}$即当a>0时f(x)在(0,$\frac{1}{a}$)上是增函数,在($\frac{1}{a}$,+∞)上是减函数.
(2)则由已知,对于任意的x1∈(1,2),总存在x2∈(1,2),
使-f(x1)=g(x2),
设h(x)=-f(x)在(1,2)的值域为A,g(x)在(1,2)的值域为B,
得A⊆B
由(1)知a=1时,h′(x)=$\frac{1-x}{x}$<0在(1,2)1上是减函数,
∴h(x)在x∈(1,2)上单调递减,
∴h(x)的值域为A=(ln2-2,-1)
∵g'(x)=bx2-b=b(x-1)(x+1)
∴(i)当b<0时,g(x)在(1,2)上是减函数,
此时,g(x)的值域为B=($\frac{2}{3}$b,-$\frac{2}{3}$b)
为满足A⊆B,又-$\frac{2}{3}$b≥0>-1
∴$\frac{2}{3}$b≤ln2-2.即b≤$\frac{3}{2}$ln2-3.
(ii)当b>0时,g(x)在(1,2)上是单调递增函数,
此时,g(x)的值域为B=(-$\frac{2}{3}$b,$\frac{2}{3}$b)
为满足A⊆B,又$\frac{2}{3}$b≥0>-1.
∴-$\frac{2}{3}$b≤ln2-2
∴b≥-$\frac{3}{2}$(ln2-2)=3-$\frac{3}{2}$ln2,
综上可知b的取值范围是(-∞,$\frac{3}{2}$ln2-3]∪[3-$\frac{3}{2}$ln2,+∞).
点评 本题主要考查函数单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{2},6$) | B. | ($\frac{3}{2},2$) | C. | (1,6) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,1) | B. | [1,4] | C. | ($\frac{1}{3}$,4] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
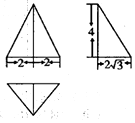
| A. | $\frac{{64\sqrt{3}}}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $\frac{32}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com