
���� ��������Բ�������ʹ�ʽ���a2=4b2�����㣨1��$\frac{\sqrt{3}}{2}$��������Բ���̣��������a��b��ֵ�����������Բ���̣�
����ֱ�߷��̣�������Բ���̣���Τ�ﶨ����ֱ�ߵ�б�ʹ�ʽ�����m2+k=1����$\left\{\begin{array}{l}{����0}\\{1-k��0}\end{array}\right.$���������k��ȡֵ��Χ���ɵ㵽ֱ�ߵľ��뼴�����k��m��ֵ�����ֱ��l�ķ��̣�
��� �⣺���������⣬e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{{\sqrt{3}}}{2}$����a2=4b2��
����Բ���㣨1��$\frac{\sqrt{3}}{2}$����������Բ���̣�$\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$��
��ã�a2=4��b2=1��
����Բ�ı����̣�$\frac{{x}^{2}}{4}+{y}^{2}=1$��
������P��x1��y1����Q��x2��y2������$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$��
�������1+4k2��x2+8kmx+4��m2-1��=0��
��x1+x2=-$\frac{8km}{1+4{k}^{2}}$��x1x2=$\frac{4��{m}^{2}-1��}{1+4{k}^{2}}$��
��kOP+kOQ=$\frac{{y}_{1}}{{x}_{1}}$+$\frac{{y}_{2}}{{x}_{2}}$=$\frac{{y}_{1}{x}_{1}+{y}_{2}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{��k{x}_{1}+m��{x}_{2}+��k{x}_{2}+m��{x}_{1}}{{x}_{1}{x}_{2}}$=2��
2��k-1��x1x2+m��x1+x2��=0��
��2��k-1����$\frac{4��{m}^{2}-1��}{1+4{k}^{2}}$+m����-$\frac{8km}{1+4{k}^{2}}$��=0��
�����ã�m2+k=1��
�ɡ�=16��4k2-m2+1��=16��4k2+k����
$\left\{\begin{array}{l}{4{k}^{2}+k��0}\\{{m}^{2}=1-k��0}\end{array}\right.$����ã�k��-$\frac{1}{k}$����0��k��1��
ֱ����Բx2+y2=1���У���$\frac{حmح}{\sqrt{1+{k}^{2}}}$=1��
�������k=0����ȥ����k=-1��
��m2=2����m=��$\sqrt{2}$��
��ֱ��l�ķ���y=x��$\sqrt{2}$��
���� ���⿼����Բ�ı����̼��������ʣ�ֱ������Բ��λ�ù�ϵ������Τ�ﶨ����ֱ�ߵ�б�ʹ�ʽ���㵽ֱ�ߵľ��빫ʽ��������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|1��x��5} | B�� | {x|x��5} | C�� | {1} | D�� | {1��5} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
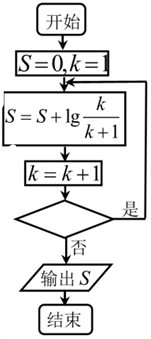
| A�� | k��8 | B�� | k��9 | C�� | k��10 | D�� | k��11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com