
���� �������������������ߵ�������� b2+c2-a2=bc�����������Ҷ������cosA��ֵ���ɵ�A��ֵ��
�������ú���y=Asin����x+�գ���ͼ��任���ɣ����g��x���Ľ���ʽ�����������Һ����Ķ������ֵ�����g��x����[0����]�ϵ�ֵ��
��� �⣺����ABC�������ڽ�A��B��C�ĶԱ߷ֱ���a��b��c��
������$\overrightarrow{m}$=��a+c��sinB����$\overrightarrow{n}$=��b-c��sinA-sinC������$\overrightarrow{m}$��$\overrightarrow{n}$��
��a+c��•��sinA-sinC��-sinB��b-c��=0������a+c��•��a-c��=b��b-c����
�� b2+c2-a2=bc����cosA=$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2bc}$=$\frac{1}{2}$����A=$\frac{��}{3}$��
�����躯��f��x��=tanAsin��xcos��x-cosAcos2��x���أ�0��=$\frac{\sqrt{3}}{2}$sin2��x-$\frac{1}{2}$cos2��x=sin��2��x-$\frac{��}{6}$����
��֪��ͼ������������Գ����ľ���Ϊ$\frac{T}{2}$=$\frac{1}{2}•\frac{2��}{2��}$=$\frac{��}{2}$�����=1��
�ֽ�y=f��x��=sin��2x-$\frac{��}{6}$����ͼ���ϸ�������ƽ��$\frac{��}{6}$����λ��
�ɵ� y=sin��2x+$\frac{��}{6}$����ͼ���ٽ�����ͼ���ϸ���ĺ������쳤Ϊԭ����2����
�õ�����y=g��x��=sin��x+$\frac{��}{6}$�� ��ͼ��
��[0����]�ϣ�x+$\frac{��}{6}$��[$\frac{��}{6}$��$\frac{7��}{6}$]��g��x��=sin��x+$\frac{��}{6}$����[-$\frac{1}{2}$��1]��
��g��x����[0����]�ϵ�ֵ��Ϊ[-$\frac{1}{2}$��1]��
���� ������Ҫ���������������ߵ����ʣ����Ҷ���������y=Asin����x+�գ���ͼ��任���ɣ����Һ����Ķ������ֵ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
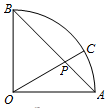 ��ͼ������AOB��Բ�Ľ�Ϊ90�㣬��P����AB�ϣ���OP=$\sqrt{2}$AP���ӳ�OP����AB�ڵ�C����������������Ͷһ�㣬��õ���������AOC�ڵĸ���Ϊ$\frac{1}{3}$��
��ͼ������AOB��Բ�Ľ�Ϊ90�㣬��P����AB�ϣ���OP=$\sqrt{2}$AP���ӳ�OP����AB�ڵ�C����������������Ͷһ�㣬��õ���������AOC�ڵĸ���Ϊ$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
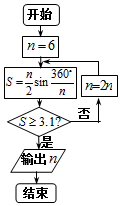 ��Ԫ263�����ң��ҹ���ѧ�����շ��ֵ�Բ�ڽ�������εı�����������ʱ���������������ޱƽ�Բ��������������ˡ���Բ���������á���Բ�������յõ���Բ���ʾ�ȷ��С�������λ�Ľ���ֵ3.14������������ġ����ʡ�����ͼ���������յġ���Բ����˼����Ƶ�һ�������ͼ�������n��ֵΪ���ο����ݣ�sin15��=0.2588��sin7.5��=0.1305����������
��Ԫ263�����ң��ҹ���ѧ�����շ��ֵ�Բ�ڽ�������εı�����������ʱ���������������ޱƽ�Բ��������������ˡ���Բ���������á���Բ�������յõ���Բ���ʾ�ȷ��С�������λ�Ľ���ֵ3.14������������ġ����ʡ�����ͼ���������յġ���Բ����˼����Ƶ�һ�������ͼ�������n��ֵΪ���ο����ݣ�sin15��=0.2588��sin7.5��=0.1305����������| A�� | 16 | B�� | 20 | C�� | 24 | D�� | 48 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y2=4x | B�� | y2=8x | C�� | y2=12x | D�� | y2=16x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
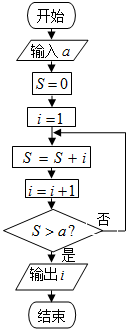
| A�� | 14 | B�� | 17 | C�� | 19 | D�� | 21 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 32 | B�� | 16 | C�� | 8 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com