考点:两角和与差的正弦函数,平行向量与共线向量,平面向量数量积的运算
专题:三角函数的求值
分析:(Ⅰ)把ω=2代入由向量
与
共线可得x的等式,可得答案;(Ⅱ)由题意结合三角函数的化简可得f(x)sin(2ωx+
)+
,可得周期,进而可得ω=1,代入条件化简可得sinα+cosα=
,平方可得sin2α=-
,由同角三角函数的基本关系可得cos2α
解答:
解:(Ⅰ)当ω=2时,
=(
sin2x,cos2x),
=(cos2x,cos2x),
∵向量
与
共线,∴
sin2xcos2x-cos
22x=0,
可得cos2x=0,或tan2x=
=
,
∵x∈(0,π),∴x=
,或x=
,或x=
;
(Ⅱ)f(x)=
•=
sinωxcosωx+cos
2ωx
=
sin2ωx+
=sin(2ωx+
)+
∵函数f(x)的图象与直线y=
的任意两个相交邻点间的距离都是
,
∴函数f(x)的周期为π,∴ω=1
∴f(x)=sin(2x+
)+
,
∵f(
+
)=sin(α+
)
+=
+
,
∴sin(α+
)=
(sinα+cosα)=
,
∴sinα+cosα=
,平方可得1+sin2α=
,
解得sin2α=-
,
cos2α=±
=±
.
点评:本题考查两角和与差的三角函数公式,涉及向量共线和三角函数的性质,属中档题.



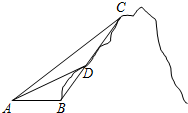 某旅游景点有一座风景秀丽的山峰,游客可以乘长为3km的索道AC上山,也可以沿山路BC上山,山路BC中间有一个距离山脚B为1km的休息点D.已知∠ABC=120°,∠ADC=150°.假设小王和小李徒步攀登的速度为每小时1.2km,请问:两位登山爱好者能否在2个小时内徒步登上山峰(即从B点出发到达C点)
某旅游景点有一座风景秀丽的山峰,游客可以乘长为3km的索道AC上山,也可以沿山路BC上山,山路BC中间有一个距离山脚B为1km的休息点D.已知∠ABC=120°,∠ADC=150°.假设小王和小李徒步攀登的速度为每小时1.2km,请问:两位登山爱好者能否在2个小时内徒步登上山峰(即从B点出发到达C点)