
| A. | (3,4) | B. | (2,3) | C. | $(\sqrt{3},4)$ | D. | $(\sqrt{3},2)$ |
分析 设右焦点F(c,0),直线l的方程为y=2(x-c),代入双曲线的方程可得(b2-4a2)x2+8ca2x-4a2c2-a2b2=0,运用韦达定理和中点坐标公式,再由条件可得2c<$\frac{4c{a}^{2}}{4{a}^{2}-{b}^{2}}$<4c,结合a,b,c的关系和离心率公式,计算即可得到所求范围.
解答 解:设右焦点F(c,0),直线l的方程为y=2(x-c),
代入双曲线的方程可得(b2-4a2)x2+8ca2x-4a2c2-a2b2=0,
设A(x1,y1),B(x2,y2),
可得x1+x2=$\frac{8c{a}^{2}}{4{a}^{2}-{b}^{2}}$,
即有AB的中点的横坐标为$\frac{4c{a}^{2}}{4{a}^{2}-{b}^{2}}$,
由题意可得2c<$\frac{4c{a}^{2}}{4{a}^{2}-{b}^{2}}$<4c,
化简可得2a2<b2<3a2,
即有3a2<c2<4a2,
即$\sqrt{3}$a<c<2a,
可得e=$\frac{c}{a}$∈($\sqrt{3}$,2).
故选:D.
点评 本题考查双曲线的离心率的范围,注意运用直线方程和双曲线的方程联立,运用韦达定理和中点坐标公式,考查化简整理的运算能力,属于中档题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
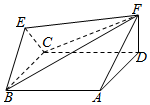 如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
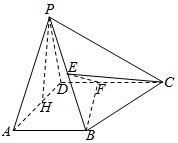 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=$\frac{1}{2}$AB,PH为△PAD中AD边上的高.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=$\frac{1}{2}$AB,PH为△PAD中AD边上的高.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-{y^2}=1$ | B. | ${x^2}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{16}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 54$\root{3}{3{π}^{2}}$ | B. | 54$\root{3}{3π}$ | C. | 54$\root{3}{12{π}^{2}}$ | D. | 54$\root{3}{12π}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com