
分析 (Ⅰ)法一:根据f(0)=0,求出a的值,
法二:根据函数的奇偶性进行判断;
(Ⅱ)求出f(x)的表达式,问题转化为t>$\frac{{2}^{x}-2}{{2}^{x}+2}$对x∈R恒成立,令g(x)=$\frac{{2}^{x}-2}{{2}^{x}+2}$,g(x)的上线,从而求出t的范围即可.
解答 解:(Ⅰ)定义域为R,又知函数为R上的奇函数,则f(0)=0⇒a=-2,
下面证明a=-2时:$f(x)=1-\frac{2}{{{2^x}+1}}$是奇函数,
∵$f(-x)=1-\frac{2}{{{2^{-x}}+1}}=1-\frac{{2•{2^x}}}{{1+{2^x}}}=\frac{{1-{2^x}}}{{1+{2^x}}}=\frac{{-({1+{2^x}})+2}}{{1+{2^x}}}=-1+\frac{2}{{1+{2^x}}}=-f(x)$,
对定义域R上的每一个x都成立,
∴f(x)为R上的奇函数,
∴存在实数a=-2,使函数f(x)为奇函数;
另解:定义域为R,又知函数为R上的奇函数,
则f(-x)=-f(x)对f(x)定义域R上的每一个x都成立.
∴$1+\frac{a}{{{2^{-x}}+1}}=-1-\frac{a}{{{2^x}+1}}$
∴$-2=\frac{a}{{{2^{-x}}+1}}+\frac{a}{{{2^x}+1}}$=$\frac{{a•{2^x}}}{{({{2^{-x}}+1})•{2^x}}}+\frac{a}{{{2^x}+1}}$=$\frac{{a•{2^x}}}{{1+{2^x}}}+\frac{a}{{{2^x}+1}}$=$\frac{{a(1+{2^x})}}{{1+{2^x}}}$=a,
∴a=-2,
∴存在实数a=-2,使函数f(x)为奇函数.
(Ⅱ)若a=1,f(x)=1+$\frac{1}{{2}^{x}+1}$,
t(2x+1)f(x)>2x-2对x∈R恒成立,
即t(2x+1)(1+$\frac{1}{{2}^{x}+1}$)>2x-2对x∈R恒成立,
即t>$\frac{{2}^{x}-2}{{2}^{x}+2}$对x∈R恒成立,
令g(x)=$\frac{{2}^{x}-2}{{2}^{x}+2}$=$\frac{1-\frac{2}{{2}^{x}}}{1+\frac{2}{{2}^{x}}}$<1,
∴t≥1.
点评 本题考查了函数画出了问题,考查函数的奇偶性以及转化思想,是一道中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,4) | B. | (2,3) | C. | $(\sqrt{3},4)$ | D. | $(\sqrt{3},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
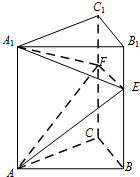 如图,正三棱柱ABC-A1B1C1中,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,则三棱锥A-A1EF的体积是8$\sqrt{3}$.
如图,正三棱柱ABC-A1B1C1中,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,则三棱锥A-A1EF的体积是8$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com