
分析 (1)利用平面向量的数量积的坐标运算可求得函数y=f(x)的表达式,由它的最小正周期为2π可求得ω的值,并求出函数y=f(x)的单调递增区间;
(2)若$0≤m≤\frac{π}{6}$,$f{(x)_{max}}=2\sqrt{3}$,$f{(x)_{min}}=f(m+\frac{π}{2})=2\sqrt{3}sin(m+\frac{5π}{6})$,此时$φ(m)=2\sqrt{3}-2\sqrt{3}sin(m+\frac{5π}{6})$,通过对$\frac{π}{6}<m≤\frac{2π}{3}$,$\frac{2π}{3}<m≤\frac{11π}{12}$,$\frac{11π}{12}<m≤π$的分类讨论,可求得函数φ(m)的解析式;
(3)由题意可知φ(m)min+g(x)min>h(x)min,对于φ(m),通过对$\frac{π}{6}<m≤\frac{2π}{3}$,$\frac{2π}{3}<m≤\frac{11π}{12}$,$\frac{11π}{12}<m≤π$的分类讨论,可求得函数φ(m)的范围$φ(m)∈[{2\sqrt{3}-\sqrt{6},2\sqrt{6}}]$,$φ{(x)_{min}}=2\sqrt{3}-\sqrt{6}$.对于h(x),由于x|x-1|≥0,且等号当x=1时能取到,$h{(x)_{min}}=2\sqrt{3}$.利用(x)>ln(1+t),可得实数t的取值范围.
解答 解:$f(x)=2\overrightarrow a•\overrightarrow b-1=2[{sinωx•(\sqrt{3}cosωx-sinωx)+2{{cos}^2}ωx}]-1$=$2(\sqrt{3}sinωx•cosωx-{sin^2}ωx+2{cos^2}ωx)-1$=$2(\frac{{\sqrt{3}}}{2}sin2ωx-\frac{1-cos2ωx}{2}+1+cos2ωx)-1$
=$2\sqrt{3}(\frac{1}{2}sin2ωx+\frac{{\sqrt{3}}}{2}cos2ωx)=2\sqrt{3}sin(2ωx+\frac{π}{3})$,
(1)∵ω>0,$T=\frac{2π}{2ω}=2π$,∴$ω=\frac{1}{2}$.∴$f(x)=2\sqrt{3}sin(x+\frac{π}{3})$,
单调递增区间由$2kπ-\frac{π}{2}≤x+\frac{π}{3}≤2kπ+\frac{π}{2}$(k∈Z),
得:$x∈[{2kπ-\frac{5π}{6},2kπ+\frac{π}{6}}],k∈Z$.
(2)若$0≤m≤\frac{π}{6}$,$f{(x)_{max}}=2\sqrt{3}$,$f{(x)_{min}}=f(m+\frac{π}{2})=2\sqrt{3}sin(m+\frac{5π}{6})$,
此时$φ(m)=2\sqrt{3}-2\sqrt{3}sin(m+\frac{5π}{6})$;
若$\frac{π}{6}<m≤\frac{2π}{3}$,$f{(x)_{max}}=f(m)=2\sqrt{3}sin(m+\frac{π}{3})$,$f{(x)_{min}}=f(m+\frac{π}{2})$=$2\sqrt{3}sin(m+\frac{5π}{6})$,此时$φ(m)=2\sqrt{3}sin(m+\frac{π}{3})-2\sqrt{3}sin(m+\frac{5π}{6})$;
若$\frac{2π}{3}<m≤\frac{11π}{12}$,$f{(x)_{max}}=f(m)=2\sqrt{3}sin(m+\frac{π}{3})$,$f{(x)_{min}}=-2\sqrt{3}$,此时$φ(m)=2\sqrt{3}sin(m+\frac{π}{3})+2\sqrt{3}$;
若$\frac{11π}{12}<m≤π$,$f{(x)_{max}}=f(m+\frac{π}{2})=2\sqrt{3}sin(m+\frac{5π}{6})$,f(x)min=$-2\sqrt{3}$,此时$φ(m)=2\sqrt{3}sin(m+\frac{5π}{6})+2\sqrt{3}$.
综上所述,$φ(m)=\left\{\begin{array}{l}2\sqrt{3}-2\sqrt{3}sin(m+\frac{5π}{6}),0≤m≤\frac{π}{6}\\ 2\sqrt{3}sin(m+\frac{π}{3})-2\sqrt{3}sin(m+\frac{5π}{6}),\frac{π}{6}<m≤\frac{2π}{3}\\ 2\sqrt{3}sin(m+\frac{π}{3})+2\sqrt{3},\frac{2π}{3}<m≤\frac{11π}{12}\\ 2\sqrt{3}sin(m+\frac{5π}{6})+2\sqrt{3},\frac{11π}{12}<m≤π\end{array}\right.$.
(3)由题意可知φ(m)min+g(x)min>h(x)min.
对于φ(m),若$0≤m≤\frac{π}{6}$,$φ(m)∈[{\sqrt{3},2\sqrt{3}}]$;若$\frac{π}{6}<m≤\frac{2π}{3}$,
φ(m)=$2\sqrt{3}sin(m+\frac{π}{3})-2\sqrt{3}sin(m+\frac{5π}{6})=2\sqrt{6}sin(m+\frac{π}{12})∈[{2\sqrt{3},2\sqrt{6}}]$;
若$\frac{2π}{3}<m≤\frac{11π}{12}$,$φ(m)∈[{2\sqrt{3}-\sqrt{6},2\sqrt{3}})$;
若$\frac{11π}{12}<m≤π$,$φ(m)∈({2\sqrt{3}-\sqrt{6},\sqrt{3}}]$.
综上所述,$φ(m)∈[{2\sqrt{3}-\sqrt{6},2\sqrt{6}}]$,$φ{(x)_{min}}=2\sqrt{3}-\sqrt{6}$.
对于h(x),由于x|x-1|≥0,且等号当x=1时能取到,∴$h{(x)_{min}}=2\sqrt{3}$.
对于g(x),不难得出g(x)>ln(1+t),
于是$φ({x_1})+g({x_2})>2\sqrt{3}-\sqrt{6}+ln(1+t)$.
∴$2\sqrt{3}-\sqrt{6}+ln(1+t)≥2\sqrt{3}$,解得:$t≥{e^{\sqrt{6}}}-1$.
点评 本题考查平面向量数量积的运算,突出考查三角函数的单调性与最值,考查等价转化思想、分类讨论思想与分析运算能力,属于难题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在侧棱长和底面边长均为2的正三棱柱ABC-A1B1C1中,点M、N、P分别在AA1、BC、BB1上运动,且AM=CN=B1P=X(0<X<2).记三棱锥P-MNB1的体积为,V(X)则函数Y=V(X)的图象大致为( )
如图,在侧棱长和底面边长均为2的正三棱柱ABC-A1B1C1中,点M、N、P分别在AA1、BC、BB1上运动,且AM=CN=B1P=X(0<X<2).记三棱锥P-MNB1的体积为,V(X)则函数Y=V(X)的图象大致为( )| A. |  | B. |  | C. | 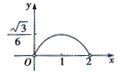 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 对服务好评 | 对服务不满意 | 合计 | |
| 对 商品 好评 | |||
| 对商品不满意 | |||
| 合 计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lnx | B. | f(x)=e-x | C. | $f(x)=\sqrt{x}$ | D. | $f(x)=-\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com