
已知⊙O:x2+y2=6,P为⊙O上动点,过P作PM⊥x轴于M,N为PM上一点,且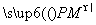 =
=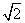
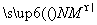 .
.
(1)求点N的轨迹C的方程;
(2)若A(2,1),B(3,0),过B的直线与曲线C相交于D,E两点,则kAD+kAE是否为定值?若是,求出该值;若不是,说明理由.
科目:高中数学 来源: 题型:
数列{an}的首项为3,{bn}为等差数列,且bn=an+1-an(n∈N*),若b3=-2,b10=12,则a8=( )
A.0 B.3
C.8 D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示的程序框图,该算法的功能是( )
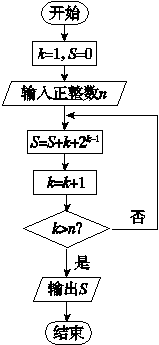
A.计算(1+20)+(2+21)+(3+22)+…+(n+1+2n)的值
B.计算(1+21)+(2+22)+(3+23)+…+(n+2n)的值
C.计算(1+2+3+…+n)+(20+21+22+…+2n-1)的值
D.计算[1+2+3+…+(n-1)]+(20+21+22+…+2n)的值
查看答案和解析>>
科目:高中数学 来源: 题型:
下列5个命题中,正确命题的个数是( )
①对于命题p:∃x∈R,使得x2+x+1<0,则綈p:∀x∈R,均有x2+x+1>0;
②m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
③已知回归直线的斜率的估计值为1.23,样本的中心点为(4,5),则回归直线方程为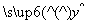 =1.23x+0.08;
=1.23x+0.08;
④若实数x,y∈[-1,1],则满足x2+y2≥1的概率为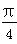 ;
;
⑤曲线y=x2与y=x所围成图形的面积是S= (x-x2)dx.
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5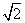 -4 B.
-4 B.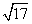 -1 C.6-2
-1 C.6-2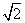 D.
D.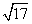
查看答案和解析>>
科目:高中数学 来源: 题型:
某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图所示的频率分布直方图.样本数据分组为[50,60),[60,70),[70,80),[80,90),[90,100].若用分层抽样的方法从样本中抽取分数在[80,100]范围内的数据16个,则其中分数在[90,100]范围内的样本数据有( )
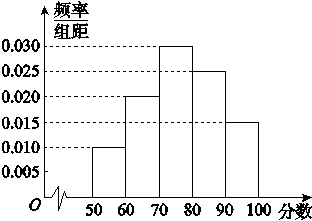
A.5个 B.6个 C.8个 D.10个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com