
 ij�̵�Ϊ�˸��õع滮ij����Ʒ�������������̵��ijһ������������У������ȡ��8��������Ϊ�о�������ͼ��ʾ��x���֣�Ϊ����Ʒ��������y���죩Ϊ������������
ij�̵�Ϊ�˸��õع滮ij����Ʒ�������������̵��ijһ������������У������ȡ��8��������Ϊ�о�������ͼ��ʾ��x���֣�Ϊ����Ʒ��������y���죩Ϊ������������| x | 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| y | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
���� �����ݱ������ݻ���ɢ��ͼ���ɣ�
�����ݱ������ݼ���$\overline{x}$��$\overline{y}$�ͻع�ϵ����д�����Իع鷽�̣�
�����ݣ��������Իع鷽�̼���x=24ʱ$\widehat{y}$��ֵ���ɣ�
��� �⣺�������ϱ����������������л���ɢ��ͼ����ͼ��ʾ��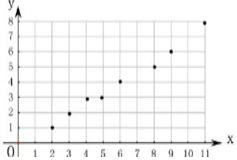
�������ϱ��ṩ�����ݣ�
����$\overline{x}$=$\frac{1}{8}$����2+3+4+5+6+8+9+11��=6��
$\overline{y}$=$\frac{1}{8}$����1+2+3+3+4+5+6+8��=4��
$\widehat{b}=\frac{{��}_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{{��}_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{241-8��6��4}{356-8{��6}^{2}}$=$\frac{49}{68}$��
$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$=4-$\frac{49}{68}$��6=-$\frac{11}{34}$��
��y����x�����Իع鷽��$\widehat{y}$=$\frac{49}{68}$x-$\frac{11}{34}$��
�����ݣ����еļ�������
x=24ʱ��$\widehat{y}$=$\frac{49}{68}$��24-$\frac{11}{34}$=$\frac{577}{34}$��17��
���Ը��̵�һ���Խ�������Ʒ24�֣�Ԥ����Ҫ����17�죮
���� ���⿼����ɢ��ͼ�����Իع鷽�̵�Ӧ�����⣬���е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [3+8k��7+8k�� | B�� | ��5+8k��7+8k] | C�� | [5+8k��7+8k�� | D�� | ��3+8k��7+8k] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-2���ȣ�2��+�ޣ� | B�� | ��-2��0���ȣ�0��2�� | C�� | ��-2��0���ȣ�2��+�ޣ� | D�� | ��-�ޣ�-2���ȣ�0��2�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com