
分析 设x1=s+ti(s,t∈R,t≠0).则x2=s-ti.则x1+x2=2s,x1x2=s2+t2.利用$\frac{x_1^2}{x_2}$是实数,可得3s2=t2.于是x1+x2=2s,x1x2=s2+t2.$(\frac{{x}_{1}}{{x}_{2}})^{2}+\frac{{x}_{1}}{{x}_{2}}$+1=0,取$\frac{{x}_{1}}{{x}_{2}}$=ω,则ω2+ω+1=0,ω3=1.代入化简即可得出.
解答 解:设x1=s+ti(s,t∈R,t≠0).则x2=s-ti.
则x1+x2=2s,x1x2=s2+t2.
∵$\frac{x_1^2}{x_2}$=$\frac{(s+ti)^{2}}{s-ti}$=$\frac{{s}^{3}-3s{t}^{2}}{{s}^{2}+{t}^{2}}$+$\frac{3{s}^{2}t-{t}^{3}}{{s}^{2}+{t}^{2}}$i是实数,
∴3s2t-t3=0,
∴3s2=t2.
∴x1+x2=2s,x1x2=s2+t2.
∴4s2=$({x}_{1}+{x}_{2})^{2}$=${x}_{1}^{2}+{x}_{2}^{2}$+2x1x2=x1x2,
∴$(\frac{{x}_{1}}{{x}_{2}})^{2}+\frac{{x}_{1}}{{x}_{2}}$+1=0,
取$\frac{{x}_{1}}{{x}_{2}}$=ω,
则ω2+ω+1=0,
∴ω3=1.
则S=1+$\frac{x_1}{x_2}+{({\frac{x_1}{x_2}})^2}+{({\frac{x_1}{x_2}})^4}+{({\frac{x_1}{x_2}})^8}+{({\frac{x_1}{x_2}})^{16}}+{({\frac{x_1}{x_2}})^{32}}$=1+ω+ω2+ω4+ω8+ω16+ω32
=0+ω+ω2+ω+ω2
=-2.
故答案为:-2.
点评 本题考查了复数的运算法则、实系数一元二次方程虚根成对原理及其根与系数的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
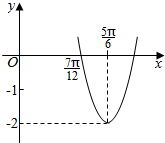
| A. | 函数f(x)在区间[0,$\frac{π}{2}$]上单调递增 | B. | 函数f(x)在区间[0,$\frac{π}{2}$]上单调递减 | ||
| C. | 函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-2 | D. | 函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②④ | B. | ①④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{5}{4}$,-$\frac{1}{2}$) | B. | (-∞,-$\frac{5}{4}$]∪(-$\frac{1}{2}$,+∞) | C. | [-$\frac{5}{4}$,1) | D. | [-$\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com