
| ����� | [0��1000] | ��1000��3000] | ��3000��+�ޣ� |
| ���� | 6 | 18 | 12 |
���� �����ִ�36���ƿ��в��÷ֲ�����ķ�ʽѡ��6�ڣ��õ�������ϵ��������ѡ���ĵ��������3000�Ľ�����
����X�Ŀ���ȡֵΪ0��20��40��60��������ʵõ��ֲ��У�Ȼ������������ɣ�
��� ����С������12�֣�
�⣺�����ݷֲ������6��18��12=1��3��2��ѡ����6�ڿ�����2�ڵ��������3000��
����X�Ŀ���ȡֵΪ0��20��40��60��
P��X=0��=$\frac{1}{{C}_{6}^{2}}$=$\frac{1}{15}$��P��X=20��=$\frac{{C}_{3}^{1}{C}_{2}^{1}}{{C}_{6}^{2}}$=$\frac{2}{5}$��P��X=40��=$\frac{{C}_{2}^{1}+{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{1}{3}$��P��X=60��=$\frac{{C}_{3}^{1}}{{C}_{6}^{2}}$=$\frac{1}{5}$��
��X�ķֲ���Ϊ��
| X | 0 | 20 | 40 | 60 |
| P | $\frac{1}{15}$ | $\frac{2}{5}$ | $\frac{1}{3}$ | $\frac{1}{5}$ |
���� ��С����Ҫ����ѧ���Գ��������⣬�Լ��ֲ��е����֪ʶ��ͬʱ����ѧ�������ݴ���������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������ABCD�У�AB=CD=4��AD=BD=5��AC=BC=6����E��F��G��H�ֱ�����AD��BD��BC��AC�ϣ���ֱ��AB��CD��ƽ����ƽ��EFGH�����ı���EFGH��������ֵ��4��
��ͼ����������ABCD�У�AB=CD=4��AD=BD=5��AC=BC=6����E��F��G��H�ֱ�����AD��BD��BC��AC�ϣ���ֱ��AB��CD��ƽ����ƽ��EFGH�����ı���EFGH��������ֵ��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
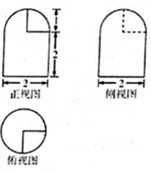 ��֪һ�������������ͼ��ͼ��ʾ����ü�����ı����Ϊ��������
��֪һ�������������ͼ��ͼ��ʾ����ü�����ı����Ϊ��������| A�� | $\frac{25}{4}$�� | B�� | 7�� | C�� | $\frac{29}{4}$�� | D�� | $\frac{31}{4}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | -8 | C�� | ��8 | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4 | B�� | 4 | C�� | -8 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|1��x��3} | B�� | {x|-1��x��3} | C�� | {x|-1��x��1} | D�� | ∅ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\frac{1}{e}$��2e] | B�� | [$\frac{1}{e}$��$\frac{2}{e}$] | C�� | [$\frac{3}{e}$��2e] | D�� | [$\frac{3}{e}$��$\frac{8}{{e}^{2}}$] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com