考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)连结AC交BD于点O,连结C1O,PO,证明C1O⊥BD,C1O⊥OP,可得C1O⊥平面PBD,即可证明平面PBD⊥平面C1BD;
(2)几何体BA1C1D的体积等于正四棱柱ABCD-A1B1C1D1的体积减去4个角落的体积.
解答:
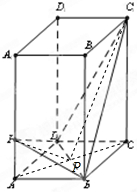
(1)证明:连结AC交BD于点O,连结C
1O,PO
∵正四棱柱ABCD-A
1B
1C
1D
1,
∴C
1C⊥平面ABCD且O为BD、AC中点,
∴C
1C⊥CD,C
1C⊥BC
又∵正四棱柱ABCD-A
1B
1C
1D
1,
∴CD=CB,∴C
1D=C
1B,
∴C
1O⊥BD
又
C1O==
,
PO===,
PC1===,
C1O2+PO2=8+===PC12∴C
1O⊥OP,
∵OP∩BD=0
∴C
1O⊥平面PBD
又∵C
1O?平面C
1BD
∴平面PBD⊥平面C
1BD…(6分)
(2)解:V
BA1C1D等于正四棱柱ABCD-A
1B
1C
1D
1的体积减去4个角落的体积,
设正四棱柱ABCD-A
1B
1C
1D
1的体积为V
∴V
BA1C1D=V-
V×4=
V=
×2×2×6=8…(12分)
点评:本题考查的知识点是平面与平面垂直的判定,体积的计算,其中熟练掌握面面垂直的判定定理及证明步骤是解答本题的关键.

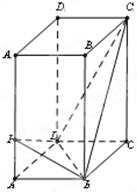 如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.
如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6. (1)证明:连结AC交BD于点O,连结C1O,PO
(1)证明:连结AC交BD于点O,连结C1O,PO

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案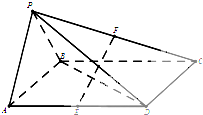 四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB=
四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB= 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=