
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、5 | ||
C、
| ||
| D、2 |
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、10 | B、8 | C、12 | D、14 |
查看答案和解析>>
科目:高中数学 来源: 题型:
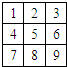 用红、黄、蓝三种颜色去涂题图中标号为1,2,…,9的9个小正方形,使得任意相邻(有公共边)的小正方形所涂的颜色不同,且“3、5、7”号数字涂色相同,则符合条件的所有涂法种数为( )
用红、黄、蓝三种颜色去涂题图中标号为1,2,…,9的9个小正方形,使得任意相邻(有公共边)的小正方形所涂的颜色不同,且“3、5、7”号数字涂色相同,则符合条件的所有涂法种数为( )| A、96 | B、108 |
| C、196 | D、432 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com