考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)把a=2代入,求出函数的导数,解不等式得到单调区间,从而求出极值,
(2)先求出函数的导数,再分别讨论①a≤0时②a>0时的情况,从而求出单调区间,
(3)将问题转化为:方程a=
在区间[
,e]上有且只有一个解,令g(x)=
,则g′(x)=
,从而解决问题.
解答:
解:(1)a=2时,f(x)=x
2-2lnx,x>0,
∴f′(x)=
,
令f′(x)>0,解得:x>1,x<-1(舍),
令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减,在(1,+∞)递增,
∴x=1时,f(x)取到极小值f(1)=1,
(2)∵f′(x)=
,x>0,
①a≤0时,f′(x)>0,f(x)在(0,+∞)递增,
②a>0时,
令f′(x)>0,解得:x>
,x<-
(舍),
令f′(x)<0,解得:0<x<
,
∴f(x)在(0,
)递减,在(
,+∞)递增;
综上:a≤0时,f(x)在(0,+∞)递增
a>0时,f(x)在(0,
)递减,在(
,+∞)递增;
(3)由题意得:方程a=
在区间[
,e]上有且只有一个解,
令g(x)=
,则g′(x)=
,
令g′(x)=0,解得:x=
,
∴g(x)在(
,
)上递减,在(
,e)递增,
又g(
)=
<g(e)=e
2,
∴方程a=
在区间[
,e]上有且只有一个解时,
有
<a≤e
2,或a=2e,
∴实数a的取值范围时:{a|
<a≤e
2或a=2e}.
点评:本题考察了函数的单调性,函数的最值问题,参数的范围,导数的应用,是一道综合题.



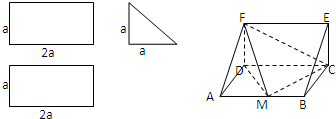 一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M是AB的中点.
一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M是AB的中点.
