
分析 (1)求函数的导数,利用f′(-1)=0,解方程即可.
(2)设出切点坐标,求出切线方程,进行求解即可得到结论.
解答 解:(1)∵f(x)=$\frac{2x}{{x}^{2}+a}$,
∴f′(x)=$\frac{2({x}^{2}+a)-2x•2x}{({x}^{2}+a)^{2}}$=$\frac{-2{x}^{2}+2a}{({x}^{2}+a)^{2}}$,
∵数f(x)=$\frac{2x}{{x}^{2}+a}$(a>0)在x=-1处的切线垂直于y轴,
∴f′(-1)=0,
即f′(-1)=$\frac{-2+2a}{(1+a)^{2}}$=0,即2a-2=0,得a=1.
(2)∵a=1,∴f(x)=$\frac{2x}{{x}^{2}+1}$,f′(x)=$\frac{-2{x}^{2}+2}{({x}^{2}+1)^{2}}$,
∵f(1)=1,∴M(1,1),
设切点P(m,$\frac{2m}{{m}^{2}+1}$),则切线斜率k=f′(m)=$\frac{2-2{m}^{2}}{({m}^{2}+1)^{2}}$,
则切线方程为y-$\frac{2m}{{m}^{2}+1}$=$\frac{2-2{m}^{2}}{({m}^{2}+1)^{2}}$(x-m),
∵切线过M(1,1),
∴1-$\frac{2m}{{m}^{2}+1}$=$\frac{2-2{m}^{2}}{({m}^{2}+1)^{2}}$•(1-m),
即$\frac{(m-1)^{2}}{{m}^{2}+1}$=$\frac{2(1-m)^{2}(1+m)}{({m}^{2}+1)^{2}}$,
即(m2+1)(m-1)2=2(1+m)(m-1)2,
若m=1,满足条件,
当m≠1时,方程等价为m2+1=2(1+m),即m2-2m-1=0,
得m=1±$\sqrt{2}$,
当m=1时,P(1,1),
当m=1+$\sqrt{2}$,P(1+$\sqrt{2}$,$\frac{\sqrt{2}}{2}$),
当m=1-$\sqrt{2}$,P(1-$\sqrt{2}$,-$\frac{\sqrt{2}}{2}$).
点评 本题主要考查导数的几何意义的应用,求函数的导数,求出函数的切线方程是解决本题的关键.考查学生的计算能力.


科目:高中数学 来源: 题型:解答题
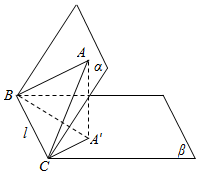 如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.
如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=-|x-1| | C. | y=ex-e-x | D. | y=ln$\frac{1-x}{1+x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com