
分析 (1)由数列距离的定义即可求得数列1,3,5,6和数列2,3,10,7的距离;
(2)由数列的递推公式,即可求得a,a3,a4,a5,求得A中数列的项周期性重复,且间隔4项重复一次,求得数列{bn}和{cn}规律,可知随着项数m越大,数列{bn}和{cn}的距离越大,由$\sum_{i=1}^{4}$=bi-ci|=$\frac{7}{3}$,根据周期的定义,得$\sum_{i=1}^{3456}$|bi-ci|=$\sum_{i=1}^{4×864}$|bi-ci|=$\frac{7}{3}$×864=2016,求得m的最大值;
(3)利用反证法,假设T中的元素个数大于等于17个,设出{cn},{dn},{fn},最总求得$\sum_{i=1}^{7}$|fi-ci|≤2和$\sum_{i=1}^{7}$|fi-di|≤2中必有一个成立,与数列的距离大于或等于3矛盾,故可证明T中的元素个数小于或等于16.
解答 解:(1)由题意可知,数列1,3,5,6和数列2,3,10,7的距离为1+0+5+1=7,
(2)设a1=p,其中p≠0,且p≠±1,
由an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$,得a2=$\frac{1+p}{1-p}$,a3=-$\frac{1}{p}$,a4=$\frac{p-1}{p+1}$,a5=p,
∴a1=a5,
因此A中数列的项周期性重复,且间隔4项重复一次,
所数列{bn}中,b4k-3=2,b4k-2=-3,b4k-1=-$\frac{1}{2}$,b4k=$\frac{1}{3}$,k∈N*,
所以{cn}中,b4k-3=3,b4k-2=-2,b4k-1=-$\frac{1}{3}$,b4k=$\frac{1}{2}$,k∈N*,
$\sum_{i=1}^{k+1}$|bi-ci|≥$\sum_{i+1}^{k}$|bi-ci|,得项数m越大,数列{bn}和{cn}的距离越大,
由$\sum_{i=1}^{4}$=bi-ci|=$\frac{7}{3}$,
得$\sum_{i=1}^{3456}$|bi-ci|=$\sum_{i=1}^{4×864}$|bi-ci|=$\frac{7}{3}$×864=2016,
所以m<3456时,$\sum_{i=1}^{m}$|bi-ci|<2016,
故m的最大值为3455,
(3)证明:假设T中的元素个数大于等于17个,
因为数列{an}中,ai=0或1,
所以仅由数列前三项组成的数组(a1,a2,a3)有且仅有8个,(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),
(1,0,1),(0,1,1),(1,1,1),
那么这17个元素(即数列)之中必有三个具有相同的a1,a2,a3,
设这个数列分别为{cn}:c1,c2,c3,c4,c5,c6,c7,{dn}:d1,d2,d3,d4,d5,d6,d7,{fn}:f1,f2,f3,f4,f5,f6,f7,
其中c1=d1=f1,c2=d2=f2,c3=d3=f3,
因为这三个数列中每两个的距离大于等于3,
所以,{bn}和{cn}中,ci=di,(i=4,5,6,7)中至少有三个成立,
不妨设c4≠d4,c5≠d5,c6≠d6,
由题意,c4和d4中一个等于0,而另一个等于1,
又因为f4=0或1,
所以f4=c4和f4=d4中必有一个成立,
同理,得f5=c5和f5=d5中必有一个成立,f6=c6和f6=d6中必有一个成立,
所以“fi=ci(i=3,4,5)中至少有两个成立”或”fi=di(i=4,5,6)中至少有两个成立“中必有一个成立,
所以$\sum_{i=1}^{7}$|fi-ci|≤2和$\sum_{i=1}^{7}$|fi-di|≤2中必有一个成立.
与题意矛盾,
∴T中的元素个数小于或等于16.
点评 本题考查数列的新定义,求数列的周期,考查反证法的应用,考查学生分析解决问题的能力,正确理解新定义是关键,属于难题.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一条直线和x轴的正方向所成的角叫该直线的倾斜角 | |
| B. | 直线的倾斜角α的取值范围是:0°≤α≤180° | |
| C. | 任何一条直线都有斜率 | |
| D. | 任何一条直线都有倾斜角 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
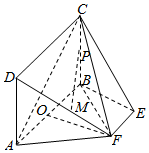 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com