考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)由已知先证明CD⊥AB,又在直三棱柱ABC-A
1B
1C
1中,AA
1⊥CD,且AB∩AA
1=A,即可证明CD⊥平面A
1ABB
1;
(Ⅱ)连结BC
1,设BC
1与B
1C的交点为E,连接DE,证得DE∥AC
1;由线面平行的判定定理即可证明AC
1∥平面CDB
1;
(Ⅲ)存在点M为B,由(Ⅰ)知CD⊥平面A
1ABB
1,又A
1B?A
1ABB
1,可得CD⊥A
1B,由已知可得A
1A:AB=BD:BB
1=1:
,即证明A
1B⊥B
1D,又CD∩B
1D=D,从而证明A
1B⊥平面CDB
1.
解答:
证明:(Ⅰ)∵AC=BC,AC⊥BC,点D是AB的中点.
∴CD=
AB,由勾股定理可得CD⊥AB,
又∵在直三棱柱ABC-A
1B
1C
1中,AA
1⊥CD,且AB∩AA
1=A,
∴CD⊥平面A
1ABB
1;
(Ⅱ)连结BC
1,设BC
1与B
1C的交点为E,连结DE.
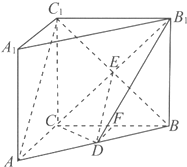
∵三棱柱ABC-A
1B
1C
1,CC
1⊥底面ABC,
CC
1=BC=2,
∴四边形BCC
1B
1为正方形.
∴E为BC
1中点.
∵D是AB的中点,
∴DE∥AC
1.
∵DE?平面CDB
1,AC
1?平面CDB
1,
∴AC
1∥平面CDB
1.
(Ⅲ)存在点M为B,证明如下:
由(Ⅰ)知CD⊥平面A
1ABB
1,又A
1B?A
1ABB
1,
∴CD⊥A
1B,
∵AC=BC=CC
1,AC⊥BC,点D是AB的中点.
∴A
1A:AB=BD:BB
1=1:
,
∴A
1B⊥B
1D,
又CD∩B
1D=D,
∴A
1B⊥平面CDB
1.
从而得证.
点评:本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,考查空间想象能力,逻辑思维能力,考查了转化思想,属于中档题.

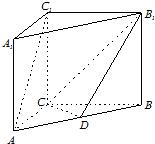 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案 方程
方程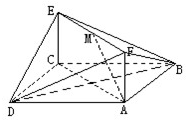 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=