
【题目】已知函数![]() .
.
(1)求![]() 在
在![]() 上的最值;
上的最值;
(2)设![]() ,若当
,若当![]() ,且
,且![]() 时,
时,![]() ,求整数
,求整数![]() 的最小值..
的最小值..
【答案】(1)详见解析(2)2
【解析】
(1)先对函数求导,然后讨论参数![]() 的范围,分别判断每种情况下
的范围,分别判断每种情况下![]() 的单调性,即可求出对应的最值;
的单调性,即可求出对应的最值;
(2)先写出![]() 的解析式,分两种情况讨论:
的解析式,分两种情况讨论:
当![]() 时,由(1)易知
时,由(1)易知![]() 时,
时,![]() ,从而
,从而![]() ,进而可得m的范围;
,进而可得m的范围;
当![]() 时,可将
时,可将![]() 变形为
变形为![]() ,只需用导数的方法研究
,只需用导数的方法研究![]() 的单调性和最值即可;
的单调性和最值即可;
解法一:
(1)![]() ,
,
①当![]() 时,
时,
因为![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,无最小值.
,无最小值.
②当![]() 时,
时,
令![]() ,解得
,解得![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
令![]() ,解得
,解得![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
所以![]() ,无最大值.
,无最大值.
③当![]() 时,
时,
因为![]() ,等号仅在
,等号仅在![]() ,
,![]() 时成立,
时成立,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,无最大值.
,无最大值.
综上,当![]() 时,
时,![]() ,无最小值;当
,无最小值;当![]() 时,
时,![]() ,无最大值;当
,无最大值;当![]() 时,
时,![]() ,无最大值.
,无最大值.
(2)![]() ,
,
当![]() 时,因
时,因![]() 为,由(1)知
为,由(1)知![]() ,所以
,所以![]() (当
(当![]() 时等号成立),所以
时等号成立),所以![]() .
.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
令![]() ,
,![]() ,已知化为
,已知化为![]() 在
在![]() 上恒成立,
上恒成立,
因为![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
又因为![]() ,
,![]() ,
,
所以存在![]() 使得
使得![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() 的最小整数值为2.
的最小整数值为2.
解法二:
(1)同解法一.
(2)![]() ,
,
①当![]() 时,因
时,因![]() 为,由(1)知
为,由(1)知![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
②当![]() 时,因为
时,因为![]() ,
,![]() ,所以
,所以![]() ,
,
令![]() ,
,![]() ,已知化为
,已知化为![]() 在
在![]() 上恒成立,
上恒成立,
因为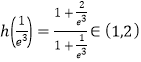 在
在![]() 上,所以
上,所以![]() ,
,
下面证明![]() ,即证
,即证![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,![]() ,
,
则![]() ,令
,令![]() ,得,
,得,
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上递减;
上递减;
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上递增,
上递增,
所以![]() ,且
,且![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() .
.
由①②得当![]() 时,
时,![]() ,
,
所以![]() 的最小整数值为2.
的最小整数值为2.


科目:高中数学 来源: 题型:
【题目】某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
周一 | 无雨 | 无雨 | 有雨 | 有雨 |
周二 | 无雨 | 有雨 | 无雨 | 有雨 |
收益 |
|
|
|
|
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为![]() 万元;有雨时,收益为
万元;有雨时,收益为![]() 万元.额外聘请工人的成本为
万元.额外聘请工人的成本为![]() 万元.
万元.
已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为![]() 万元的概率为
万元的概率为![]() .
.
(Ⅰ)若不额外聘请工人,写出基地收益![]() 的分布列及基地的预期收益;
的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
: (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市政府为做好![]() 会议接待服务工作,对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测,只有两轮都合格才能进行销售,否则不能销售.已知该海产品第一轮检测不合格的概率为
会议接待服务工作,对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测,只有两轮都合格才能进行销售,否则不能销售.已知该海产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.
(1)求该海产品不能销售的概率.
(2)如果该海产品可以销售,则每件产品可获利40元;如果该海产品不能销售,则每件产品亏损80元(即获利-80元).已知一箱中有该海产品4件,记一箱该海产品获利![]() 元,求
元,求![]() 的分布列,并求出数学期望
的分布列,并求出数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的
上每一点的横坐标保持不变,纵坐标变为原来的![]() ,得曲线
,得曲线![]() .
.
(1)求出![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设
轴正半轴为极轴建立极坐标系,设![]() 是曲线
是曲线![]() 上的一个动点,求点
上的一个动点,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列![]() 中,已知公差
中,已知公差![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)求![]() .
.
【答案】(1)![]() ;(2)100
;(2)100
【解析】试题分析:(1)根据题意![]() ,
, ![]() ,
, ![]() 成等比数列得
成等比数列得![]() 得
得![]() 求出d即可得通项公式;(2)求项的绝对前n项和,首先分清数列有多少项正数项和负数项,然后正数项绝对值数值不变,负数项绝对值要变号,从而得
求出d即可得通项公式;(2)求项的绝对前n项和,首先分清数列有多少项正数项和负数项,然后正数项绝对值数值不变,负数项绝对值要变号,从而得![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,∴
,∴![]()
![]()
![]()
![]() 计算 即可得出结论
计算 即可得出结论
解析:(1)由题意可得,则![]() ,
, ![]() ,
,
![]() ,即
,即![]() ,
,
化简得![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
(2)由(1)得![]() 时,
时,
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() .
.
∴![]() .
.
点睛:对于数列第一问首先要熟悉等差和等比通项公式及其性质即可轻松解决,对于第二问前n项的绝对值的和问题,首先要找到数列由多少正数项和负数项,进而找到绝对值所影响的项,然后在求解即可得结论
【题型】解答题
【结束】
18
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com