
分析 利用定积分,列出关于面积的式子,求出a,再利用二项式定理求系数的方法求解.
解答 解:已知抛物线y2=ax(a>0)与直线x=1围成的封闭图形的面积为$\frac{4}{3}$,
利用定积分,面积S=∫01[$\sqrt{ax}$-(-$\sqrt{ax}$)]dx=∫012$\sqrt{ax}$dx=$\frac{4}{3}$$\sqrt{a}$=$\frac{4}{3}$,得a=1,
利用二项式定理求系数的方法,Tr+1=C20r•x20-2r,
依题意令20-2r=-16,得r=18,即二项式展开式中含x-16项的系数为C2018=190.
故答案为190.
点评 本题考查定积分在求面积中的应用及利用二项式定理求二项式系数的试题.


科目:高中数学 来源: 题型:解答题
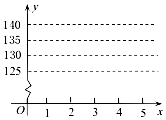 某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数y与当天气温(平均温度)x/°C的对比表:
某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数y与当天气温(平均温度)x/°C的对比表:| x | 0 | 1 | 3 | 4 |
| y | 140 | 136 | 129 | 125 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 456 | 424 | y |
| 男生 | 644 | x | z |
| A. | 16 | B. | 18 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,x2+x≤0 | B. | ?x≤0,x2+x>0 | C. | ?x0>0,x02+x0≤0 | D. | ?x0≤0,x02+x0>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1” | |
| B. | 命题“若α>β,则sinα>sinβ”的逆否命题为真命题 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,都有x2+x+1>0” | |
| D. | “x>1”是“x2+x-2>0”的充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com