
| �װ� | �Ұ� | �ϼ� | |
| ���� | 14 | 8 | 22 |
| ������ | 6 | 12 | 18 |
| �ϼ� | 20 | 20 | 40 |
| P��x2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
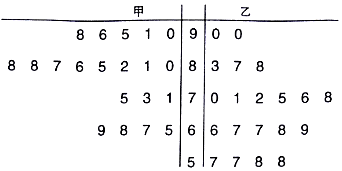
���� ��1���ɾ�Ҷͼ�ɵñ�����ɵ�K2�Ľ���ֵ����ϲο���ֵ�ɵý��ۣ�
��2��������ɵæεĿ���ֵ���ֱ��������ʣ��ɵ÷ֲ��У������ɵ���ѧ������
��� �⣺��1����ͼ��ʾ
| �װ� | �Ұ� | �ϼ� | |
| ���� | 14 | 8 | 22 |
| ������ | 6 | 12 | 18 |
| �ϼ� | 20 | 20 | 40 |
| X | 0 | 1 | 2 | 3 |
| P | $\frac{4}{35}$ | $\frac{18}{35}$ | $\frac{12}{35}$ | $\frac{1}{35}$ |
���� ���⿼�龥Ҷͼ�����ʷֲ��к���ѧ�������Լ������Լ��飬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
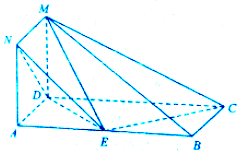 ��ͼ��������ADMN�����ABCD���ڵ�ƽ�����ֱ��AB=2AD=6����EΪ�߶�AB��һ�㣮
��ͼ��������ADMN�����ABCD���ڵ�ƽ�����ֱ��AB=2AD=6����EΪ�߶�AB��һ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | c��a��b | C�� | a��c��b | D�� | c��b��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\frac{{2\sqrt{3}}}{3}$ | C�� | $\sqrt{3}$��$\frac{{2\sqrt{3}}}{3}$ | D�� | 2��$\frac{{2\sqrt{3}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-$\frac{3}{2}$��2+y2=$\frac{25}{4}$ | B�� | ��x+$\frac{3}{4}$��2+y2=$\frac{25}{16}$ | C�� | ��x-$\frac{3}{4}$��2+y2=$\frac{25}{16}$ | D�� | ��x-$\frac{3}{4}$��2+y2=$\frac{25}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��3�� | B�� | ��1��4�� | C�� | ��2��3�� | D�� | ��2��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
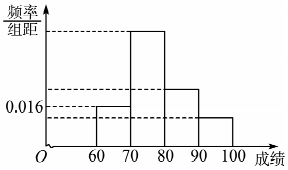 ij��Ϊ�����ѧ��ѧϰӢ�����Ȥ���ڰ��ھ���Ӣ��д��˵�����ۺ�����������������ΪԤ���;���2���Σ�Ԥ��Ϊ���ԣ�����Ϊ˵Ӣ���Ӣ������������вμӱ��Ե�ͬѧ����ͳ�ƣ��õ�Ƶ�ʷֲ�ֱ��ͼ�����к��������θ߶�֮������Ϊ4��2��1������[80��90��������Ϊ12�ˣ�
ij��Ϊ�����ѧ��ѧϰӢ�����Ȥ���ڰ��ھ���Ӣ��д��˵�����ۺ�����������������ΪԤ���;���2���Σ�Ԥ��Ϊ���ԣ�����Ϊ˵Ӣ���Ӣ������������вμӱ��Ե�ͬѧ����ͳ�ƣ��õ�Ƶ�ʷֲ�ֱ��ͼ�����к��������θ߶�֮������Ϊ4��2��1������[80��90��������Ϊ12�ˣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{2}$ | B�� | $-\frac{5}{2}$ | C�� | $\frac{5}{4}$ | D�� | $-\frac{5}{4}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com