
分析 由N(x)的性质可得知,当x是奇数时,x的最大奇数因子明显是它本身.因此N(x)=x,当x是偶数时,可将Sn进行分解,分别算出奇数项的和与偶数项的和进而相加,即Sn=S奇+S偶,由于S奇=N(1)+N(3)+…+N(2n-1)=1+3+…2n-1=4n-1,当x是偶数时,且x∈[2k,2k+1),通过分类讨论可得:当x∈[2k,2k+1)该区间所有偶数的最大奇因数和Tk=4k-1.可得S偶=T1+T2+…+Tn-1+N(2n)=$\frac{{4}^{n-1}+2}{3}$,即可得出.
解答 解:由N(x)的性质可得知,当x是奇数时,x的最大奇数因子明显是它本身.因此N(x)=x,当x是偶数时,可将Sn进行分解,分别算出奇数项的和与偶数项的和进而相加,即Sn=S奇+S偶,
∴S奇=N(1)+N(3)+…+N(2n-1)=1+3+…2n-1=$\frac{1+{2}^{n}-1}{2}×{2}^{n-1}$=4n-1,
当x是偶数时,且x∈[2k,2k+1),
①当k=1时,x∈[2,4)该区间包含的偶数只有2,而N(2)=1所以该区间所有的偶数的最大奇因数之和为T1=1,
②当k=2时,x∈[4,8),该区间包含的偶数为4,6,所以该区间所有的最大奇因数偶数之和为T2=1+3=4,
③当k=3时,x∈[8,16),该区间包含的偶数为8,10.,12,14,则该区间所有偶数的最大奇因数之和为T3=1+3+5+7=16,
因此我们可以用数学归纳法得出当x∈[2k,2k+1)该区间所有偶数的最大奇因数和Tk=4k-1.
∴对k从1到n-1求和得T1+T2+…+Tn-1=$\frac{{4}^{n-1}-1}{3}$,
∴S偶=T1+T2+…+Tn-1+N(2n)=$\frac{{4}^{n-1}+2}{3}$
综上可知Sn=S奇+S偶=4n-1+$\frac{{4}^{n-1}+2}{3}$=$\frac{{4}^{n}+2}{3}$.
∴Sn-Sn-1=$\frac{{4}^{n}+2}{3}$-$\frac{{4}^{n-1}+2}{3}$=4n-1.
∴数列{Sn-Sn-1}(n≥2)的前n项和Rn=(Sn-Sn-1)+(Sn-1-Sn-2)+…+(S2-S1)
=4n-1+4n-2+…+4
=$\frac{4({4}^{n-1}-1)}{3}$
=$\frac{{4}^{n}-4}{3}$.
故答案为:Rn=$\frac{{4}^{n}-4}{3}$.
点评 本题考查了新定义、等差数列与等比数列的通项公式及其前n项和公式、分类讨论思想方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
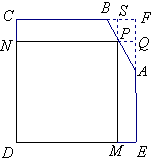 有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2.
有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 10 | B. | 10+$\sqrt{3}$ | C. | 12+$\sqrt{2}$ | D. | 12+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 执行如图所示的程序框图,输出的结果为a,二项式${({\sqrt{m}{x^2}+\frac{1}{{\sqrt{x}}}})^4}$的展开式中x3项的系数为$\frac{a}{2}$,则常数m=$\frac{1}{4}$.
执行如图所示的程序框图,输出的结果为a,二项式${({\sqrt{m}{x^2}+\frac{1}{{\sqrt{x}}}})^4}$的展开式中x3项的系数为$\frac{a}{2}$,则常数m=$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com