
分析 (Ⅰ)先求出函数f(x)的导数,通过讨论k的奇偶性,从而得到函数的单调区间;(Ⅱ)先求出函数的导数,利用倒叙相加从而证出结论.
解答 解:(Ⅰ)由已知得x>0且${f^/}(x)=2x-{(-1)^k}•\frac{2}{x}$,
当k为奇数时,则f′(x)>0,则f(x)在(0,+∞)上是增函数,
当k为偶数时,则${f^/}(x)=2x-\frac{2}{x}=\frac{2(x+1)(x-1)}{x}$,
所以当x∈(0,1)时,f′(x)<0,当x∈(1,+∞)时,f′(x)>0,
故当k为偶数时,f(x)在(0,1)上是减函数,在(1,+∞)上是增函数.
(Ⅱ)由已知得,${f^/}(x)=2x+\frac{2}{x}$(x>0),
所以左边=${(2x+\frac{2}{x})^n}-{2^{n-1}}•(2{x^n}+\frac{2}{x^n})$
=${2^n}(C_n^1{x^{n-2}}+C_n^2{x^{n-4}}+…+C_n^{n-2}\frac{1}{{{x^{n-4}}}}+C_n^{n-1}\frac{1}{{{x^{n-2}}}})$,
令S=$C_n^1{x^{n-2}}+C_n^2{x^{n-4}}+…+C_n^{n-2}\frac{1}{{{x^{n-4}}}}+C_n^{n-1}\frac{1}{{{x^{n-2}}}}$,
倒序相加得$2S=C_n^1({x^{n-2}}+\frac{1}{{{x^{n-2}}}})+C_n^2({x^{n-4}}+\frac{1}{{{x^{n-4}}}})+…+C_n^{n-2}(\frac{1}{{{x^{n-4}}}}+{x^{n-4}})+C_n^{n-1}(\frac{1}{{{x^{n-2}}}}+{x^{n-2}})$
≥2$(C_n^1+C_n^2+…+C_n^{n-2}+C_n^{n-1})$
=2(2n-2),可得S≥(2n-2),
所以:[f′(x)]n-2n-1f′(xn)≥2n(2n-2),成立.
点评 本题考查了函数的单调性问题,考查导数的应用,考查不等式的证明,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | |
| B. | 直角三角形 | |
| C. | 钝角三角形 | |
| D. | 可能是锐角三角形,也可能是钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
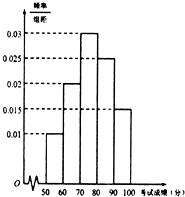 某市为了了解本地高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].
某市为了了解本地高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [1n3,+∞) | C. | [1,ln3] | D. | [-1,ln3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | -120 | C. | -240 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com