
| A. | 12π | B. | 32π | C. | 36π | D. | 48π |
分析 由题意推出MN⊥平面SAC,即SB⊥平面SAC,∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球,正方体的对角线就是球的直径,求出直径即可求出球的体积.
解答 解:∵M,N分别为棱SC,BC的中点,∴MN∥SB
∵三棱锥S-ABC为正棱锥,
∴SB⊥AC(对棱互相垂直)
∴MN⊥AC
又∵MN⊥AM,而AM∩AC=A,
∴MN⊥平面SAC,
∴SB⊥平面SAC
∴∠ASB=∠BSC=∠ASC=90°
以SA,SB,SC为从同一定点S出发的正方体三条棱,
将此三棱锥补成以正方体,则它们有相同的外接球,
正方体的对角线就是球的直径.
∴2R=$\sqrt{3}$SA=6,
∴R=3,
∴V=$\frac{4}{3}$πR3=36π.
故选:C.
点评 本题考查了三棱锥的外接球的体积,考查空间想象能力.三棱锥扩展为正方体,它的对角线长就是外接球的直径,是解决本题的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{C}_{3}^{2}}{{C}_{50}^{2}}$ | B. | $\frac{{C}_{3}^{1}{C}_{47}^{1}}{{C}_{50}^{2}}$ | C. | $\frac{{C}_{47}^{2}}{{C}_{50}^{2}}$ | D. | 1-$\frac{{C}_{47}^{2}}{{C}_{50}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=B | B. | B=A∪C | C. | B=A∩C | D. | B⊆C |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
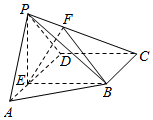 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14π | B. | 12π | C. | 10π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{4}{3})$ | B. | $(0,\frac{4}{3}]$ | C. | $\{\frac{1}{3},1,\frac{4}{3}\}$ | D. | $\{\frac{1}{3},1\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,$\frac{1}{2}$] | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{30}$ | B. | $2\sqrt{30}$ | C. | $\sqrt{51}$ | D. | $2\sqrt{51}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com