考点:直线与平面所成的角,异面直线及其所成的角
专题:空间角
分析:(1)分别以CA、CB、CC1所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出直线BC1与A1D所成角的大小.
(2)求出平面A1CD的一个法向量,利用向量法能求出直线A1E与平面A1CD所成角的正弦值.
解答:
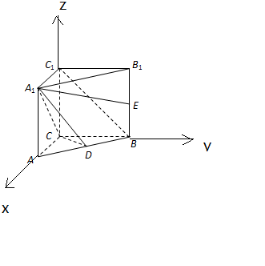
(本小题满分14分)
(理)(1)解:分别以CA、CB、CC
1所在直线为x,y,z轴,
建立空间直角坐标系.
则由题意可得:A(2,0,0),B(0,2,0),C(0,0,0),
A
1(2,0,2),B
1(0,2,2),C
1(0,0,2),
又∵D,E分别是AB,BB
1的中点,
∴D(1,1,0),E(0,2,1).…(3分)
∴
=(0,-2,2),
=(-1,1,-2),
∴
cos?,>===-,…(7分)
∴直线BC
1与A
1D所成角的大小为
.…(8分)
(2)设平面A
1CD的一个法向量为
=(x,y,z),
由
,得
,∴
=(1,-1,-1),…(10分)
又∵
=(-2,2,-1),
∴
cos?,>===-,…(13分)
∴直线A
1E与平面A
1CD所成角的正弦值为
.…(14分)
点评:本题考查直线与平面所成角的正弦值的求法,考查异面直线所成角的大小的求法,解题时要认真审题,注意向量法的合理运用.

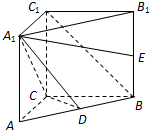 (理科)如图,在直三棱柱ABC-A1B1C1中,∠ACB=
(理科)如图,在直三棱柱ABC-A1B1C1中,∠ACB= (本小题满分14分)
(本小题满分14分)

 一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率都是
一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率都是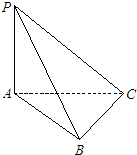 如图,已知PA⊥平面ABC,AB⊥BC,若PA=2,AB=1,BC=
如图,已知PA⊥平面ABC,AB⊥BC,若PA=2,AB=1,BC=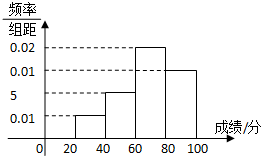 学校组织学生参加模块测试,测试后随机抽查部分学生的成绩,成绩的频率分布直方图如图5,数据的分组依次为[20,40),[40,60),[60,80),[80,100],低于60分的人数是6人
学校组织学生参加模块测试,测试后随机抽查部分学生的成绩,成绩的频率分布直方图如图5,数据的分组依次为[20,40),[40,60),[60,80),[80,100],低于60分的人数是6人