
分析 使用和角的正弦公式展开,合并,再利用二倍角公式与和角的正弦公式化简,结合正弦函数的图象与性质求出周期和最值.
解答 解:f(x)=sinx[sinx-($\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx)]=sinx($\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$cosx)=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$sinxcosx
=$\frac{1}{4}$(1-cos2x)-$\frac{\sqrt{3}}{4}$sin2x=$\frac{1}{4}$-$\frac{1}{2}$($\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x)=$\frac{1}{4}$-$\frac{1}{2}$sin(2x+$\frac{π}{6}$).
∴f(x)的最小正周期T=$\frac{2π}{2}$=π.f(x)的最小值为$\frac{1}{4}$-$\frac{1}{2}$=-$\frac{1}{4}$,f(x)的最大值为$\frac{1}{4}+\frac{1}{2}$=$\frac{3}{4}$.
点评 本题考查了三角函数的恒等变换和正弦函数的图象与性质,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -2$\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.若蛋糕店一天制作17个生日蛋糕.
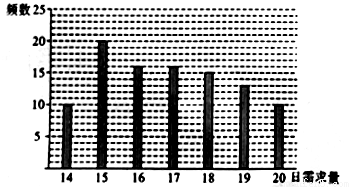
(1)求当天的利润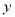 (单位:元)关于当天需求量
(单位:元)关于当天需求量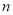 (单位:个,
(单位:个,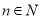 )的函数解析式;
)的函数解析式;
(2)求当天的利润不低于750元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com