
分析 根据函数的单调性将不等式组进行转化,结合线性规划的知识进行求解即可.
解答  解:∵f(x)=-f(2-x),∴-f(x)=f(2-x),
解:∵f(x)=-f(2-x),∴-f(x)=f(2-x),
∴f(a2-6a+23)+f(b2-8b)≤0可化为f(a2-6a+23)≤-f(b2-8b)=f(2-b2+8b),
又∵f(x)在R上单调递增,∴a2-6a+23≤2-b2+8b,
即a2-6a+23+b2-8b-2≤0,配方可得(a-3)2+(b-4)2≤4,
∴原不等式组可化为(x+2y)a2+2a+2xy-34≥0,
如图,点(a,b)所对应的区域为以(3,4)为圆心,2为半径的右半圆(含边界),
易知a2+b2表示点(a,b)到点(0,0)的距离的平方,
由图易知:|OA|2≤a2+b2≤|OB|2,可得点A(3,2),圆心C(3,4),
∴|OA|2=32+22=13,|OC|=5,
则最大值为(|OC|+2)2=72=49
∴13≤m2+n2≤49,即m2+n2的取值范围为[13,49].
故答案为:[13,49]
点评 本题主要考查函数单调性的应用以及线性规划的应用,根据单调性将不等式进行转化是解决本题的关键.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (3,4) | C. | (2,4] | D. | (2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 24种 | C. | 36种 | D. | 72种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频率 | |
| 男生 | 女生 | |
| [80,90] | 0 | 0.02 |
| [90,100] | 0.04 | 0.08 |
| [100,110] | 0.06 | 0.12 |
| [110,120] | 0.10 | 0.18 |
| [120,130] | 0.18 | 0.10 |
| [130,140] | 0.08 | 0.04 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
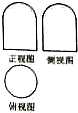 一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )| A. | 5π | B. | 6π | C. | 7π | D. | 9π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $\sqrt{66}$ | C. | 8 | D. | $\sqrt{88}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com