Question

5．在△ABC中，已知$\overrightarrow{AB}•\overrightarrow{AC}=9，sinB=cosAsinC$，S_△ABC=6，P为线段AB上的点，且$\overrightarrow{CP}=x\frac{{\overrightarrow{CA}}}{{|{\overrightarrow{CA}}|}}+y\frac{{\overrightarrow{CB}}}{{|{\overrightarrow{CB}}|}}$，
则$\overrightarrow{CP}•\overrightarrow{BP}$的最小值为$-\frac{64}{25}$．

Answer 1

分析 设AB=c，BC=a，AC=b，由sinB=cosA•sinC结合三角形的内角和及和角的正弦公式化简可求 C=90°，再由 $\overrightarrow{AB}•\overrightarrow{AC}$=9，S_△ABC=6，可求得c=5，b=3，a=4，考虑建立直角坐标系，由P为线段AB上的一点，则存在实数λ使得 $\overrightarrow{CP}$=λ$\overrightarrow{CA}$+（1-λ）$\overrightarrow{CB}$=（3λ，4-4λ）（0≤λ≤1），设出单位向量$\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}$=$\overrightarrow{{e}_{1}}$，$\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}$=$\overrightarrow{{e}_{2}}$，$\overrightarrow{{e}_{1}}$=（1，0），$\overrightarrow{{e}_{2}}$=（0，1）推出x=3λ，y=4-4λ则4x+3y=12，从而转化为一元二次函数可求最小值．

解答 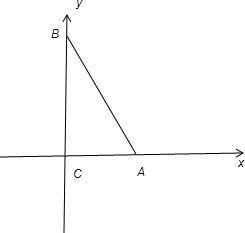解：△ABC中设AB=c，BC=a，AC=b，
∵sinB=cosA•sinC，
∴sin（A+C）=sinCcosnA，
即sinAcosC+sinCcosA=sinCcosA，
∴sinAcosC=0，∵sinA≠0，∴cosC=0，C=90°，
∵$\overrightarrow{AB}•\overrightarrow{AC}$=9，S_△ABC=6，
∴bccosA=9，$\frac{1}{2}$bcsinA=6，
∴tanA=$\frac{4}{3}$，根据直角三角形可得sinA=$\frac{4}{5}$，cosA=$\frac{3}{5}$，bc=15，
∴c=5，b=3，a=4，
以AC所在的直线为x轴，以BC所在的直线为y轴建立直角坐标系可得C（0，0）A（3，0）B（0，4），
P为线段AB上的一点，则存在实数λ使得 $\overrightarrow{CP}$=λ$\overrightarrow{CA}$+（1-λ）$\overrightarrow{CB}$=（3λ，4-4λ）（0≤λ≤1），
设$\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}$=$\overrightarrow{{e}_{1}}$，$\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}$=$\overrightarrow{{e}_{2}}$，则|$\overrightarrow{{e}_{1}}$|=|$\overrightarrow{{e}_{2}}$|=1，$\overrightarrow{{e}_{1}}$=（1，0），$\overrightarrow{{e}_{2}}$=（0，1），
由$\overrightarrow{CP}$=x•$\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}$+y•$\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}$=（x，0）+（0，y）=（x，y），
∴x=3λ，y=4-4λ，则4x+3y=12，
∴可得x=3-$\frac{3y}{4}$，
∴$\overrightarrow{CP}•\overrightarrow{BP}$=（x，y）•（x，y-4）=x²+y²-4y=（3-$\frac{3y}{4}$）²+y²-4y=$\frac{25{y}^{2}}{16}-\frac{17y}{2}+9$，
∴可解得：$\overrightarrow{CP}•\overrightarrow{BP}$的最小值为-$\frac{64}{25}$．
故答案为：-$\frac{64}{25}$．

点评 本题是一道构思非常巧妙的试题，综合考查了三角形的内角和定理、两角和的正弦公式及基本不等式求解最值问题，解题的关键是理解把已知所给的向量关系，建立x，y与λ的关系，解决本题的第二个关键点在于由x=3λ，y=4-4λ发现4x+3y=12为定值，从而转化为一元二次函数可求最小值．本题考查了平面向量及应用，考查了转化思想，属于中档题．