
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
分析 求定积分得到函数f(x)的解析式,构造奇函数g(x)=$\frac{{e}^{x}-1}{{e}^{x}+1}+ln(\sqrt{{x}^{2}+1}+x)+sinx$,由于奇函数图象的对称性,得到函数值域的对称,再对应研究函数f(x)的值域,得到本题结论.
解答 解:f(x)=$\frac{2{e}^{x}}{{e}^{x}+1}$+ln($\sqrt{{x}^{2}+1}$+x)+${∫}_{0}^{x}$cos xdx
=$\frac{2{e}^{x}}{{e}^{x}+1}$+ln($\sqrt{{x}^{2}+1}$+x)+$sinx{|}_{0}^{x}$
=$\frac{2{e}^{x}}{{e}^{x}+1}$+ln($\sqrt{{x}^{2}+1}$+x)+sinx
=$\frac{2{e}^{x}}{{e}^{x}+1}-1+ln(\sqrt{{x}^{2}+1}+x)+sinx+1$.
令g(x)=$\frac{{e}^{x}-1}{{e}^{x}+1}+ln(\sqrt{{x}^{2}+1}+x)+sinx$,定义域为R,
又g(-x)=$\frac{{e}^{-x}-1}{{e}^{-x}+1}+ln(\sqrt{{x}^{2}+1}-x)+sin(-x)$
=$\frac{\frac{1}{{e}^{x}}-1}{\frac{1}{{e}^{x}}+1}+ln\frac{1}{\sqrt{{x}^{2}+1}+x}-sinx$
=-$\frac{{e}^{x}-1}{{e}^{x}+1}-ln(\sqrt{{x}^{2}+1}+x)-sinx$
=-g(x).
∴g(x)为奇函数,
∵f(x)=g(x)+1,
∴g(x)=f(x)-1,
∵f(x)在区间[-k,k](k>0)上的值域为[m,n],
∴当f(x)取得最大值n时,g(x)也取得最大值g(x)max=n-1,
f(x)取得最小值m时,g(x)也取得最小值g(x)min=m-1,
∵函数g(x)的图象关于原点对称,
∴函数g(x)在区间[-k,k](k>0)上的最大值和最小值互为相反数,
即g(x)max+g(x)min=n-1+m-1=0,
∴m+n=2.
故选:B.
点评 本题考查定积分的求法,考查了奇函数的对称性和值域,构造奇函数,利用奇函数在对称区间上最值互为相反数建立方程进行求解是解决本题的关键,是中档题.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [0,+∞) | C. | (1,+∞) | D. | [0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{13}{4}$ | C. | $\frac{9}{4}$ | D. | $\frac{\sqrt{13}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 12 | C. | 15 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 9 | B. | -6 27 | C. | -12 9 | D. | -12 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},+∞})$ | B. | (0,+∞) | C. | (-1,+∞) | D. | .$({-\frac{1}{3},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
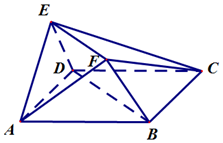 如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB=$\sqrt{2}$EA=$\sqrt{2}$ED,EF∥BD
如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB=$\sqrt{2}$EA=$\sqrt{2}$ED,EF∥BD查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $\frac{10}{3}$ | C. | 6 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
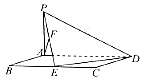 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥平面ABCD,PA=2,E,F分别为BC,PE的中点.
如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥平面ABCD,PA=2,E,F分别为BC,PE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com