
分析 (Ⅰ)根据交集的定义列出方程组,解方程组求出m的值;
(Ⅱ)归纳法猜想得出12+22+…+n2=$\frac{n(n+1)(2n+1)}{6}$(n∈N*),再用数学归纳法证明即可.
解答 解:(Ⅰ)由M={1,2,(m2-3m-1)+(m2-5m-6)i},N={3,-1},
且M∩N={3},
得(m2-3m-1)+(m2-5m-6)i=3,
所以,m2-3m-1=3且m2-5m-6=0,---(2分)
解得m=-1;---(4分)
(Ⅱ)归纳猜想,得12+22+…+n2=$\frac{n(n+1)(2n+1)}{6}$(n∈N*);---(6分)
证明:(1)当n=1时,12=$\frac{1}{6}$×1×2×3,猜想成立;
(2)假设n=k(k≥1,且k∈N*)时,猜想成立,
即12+22+…+k2=$\frac{k(k+1)(2k+1)}{6}$,
那么当n=k+1时,
12+22+…+k2=$\frac{k(k+1)(2k+1)}{6}$+(k+1)2
=$\frac{(k+1)(k+2)(2k+3)}{6}$
=$\frac{(k+1)[(k+1)+1][2k(+1)+1]}{6}$,(k∈N*),
所以,当n=k+1时,猜想成立;
由(1)(2)可知,对任意的正整数n,猜想都成立.---(12分)
点评 本题考查了交集的定义与运算问题,也考查了数学归纳法的应用问题,是综合性题目.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:解答题
已知函数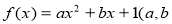 为实数),设
为实数),设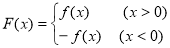
(1)若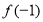 = 0且对任意实数
= 0且对任意实数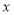 均有
均有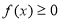 成立,求
成立,求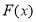 表达式;
表达式;
(2)在(1)的条件下,当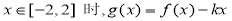 是单调函数,求实数
是单调函数,求实数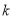 的取值范围;
的取值范围;
(3)设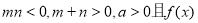 满足
满足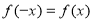 ,试比较
,试比较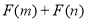 的值与0的大小.
的值与0的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π2a3 | B. | π2a3 | C. | $\frac{{π}^{2}}{2}$a3 | D. | $\frac{{π}^{2}}{3}$a3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com